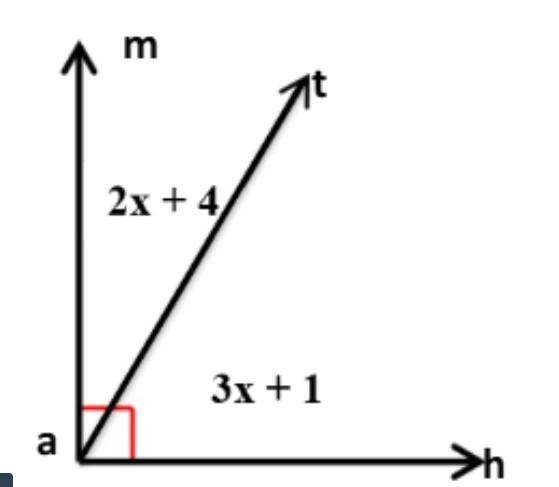
What kind of angle is
∠mah?
What is the value of x?
What is the measure of
∠mat ?
What is the measure of
∠tah ?
Answers
So according to the given figure ∠mah is right angle(90°), The value of x is 17, ∠mat is 38° and ∠tah is equal to 52°.
What is the source of this answer and define a graph?(A) ∠mah is right angle(90°) [GIVEN IN THE FIGURE]
(B) (2x+4)+(3x+1) = 90
5x+5 = 90
x= 17
(C) 2x+4 = 2×17 + 4 = 38°
(D) 3X + 1 = 3 × 17 + 1 = 52°
A graph is a visual representation or diagram that displays facts or values in an organised manner in mathematics. The points on a graph are typically used to depict the relationships between two or more things.
A graph in discrete mathematics is made up of vertices, which are groups of points, and edges, which are the connections between those vertices. There are numerous different types of graphs besides linked and disconnected graphs, weighted graphs, bipartite graphs, directed and undirected graphs, and simple graphs.
To know more about Graph, visit:
https://brainly.com/question/30444906
#SPJ1
Related Questions
A partial table of nutrients and Daily Values (DVS)
based on a 2000-calorie diet is provided. The Sodium row and the Vitamin D row are completed, and each % of the DV is calculated.
Compare each amount with the amount on the given nutrition label. Now use the amount of
saturated fat on the nutrition label to calculate its
% of DV, X. Use the saturated fat amount on the nutrition label
to calculate the %DV for saturated fat.
Answers
Note that the %DV for saturated fat in this 2 tbsp serving size is approximately 18%.
What is the explanation for the above response?To calculate the %DV for saturated fat, we need to first calculate how many grams of saturated fat are in the 2 tablespoon (tbsp) serving size.
From the label, we see that the serving size contains 3.5g of saturated fat.
To calculate the %DV for saturated fat, we use the equation:
%DV = (amount of nutrient per serving / DV) x 100%
Plugging in the values for saturated fat, we get:
%DV = (3.5g / 19g) x 100%
%DV = 0.1842 x 100%
%DV ≈ 18%
Therefore, the %DV for saturated fat in this 2 tbsp serving size is approximately 18%.
Learn more about %DV at:
https://brainly.com/question/14046971
#SPJ1
The most important of the Shinto gods is the sun goddess who gave light to the world, named ______.
Amaterasu
Susanoo
Tsukyomi
Izanagi
Answers
Answer: Amaterasu
Step-by-step explanation: The sun goddess Amaterasu is considered the most important of the Shinto gods because she is believed to be the ancestor of the Japanese imperial family, and therefore the protector of the Japanese people. She is also associated with agriculture, which was a vital part of Japanese society.
HELP RAAHHHH
1. During halftime of a football game, a sing shot launches T-shirts at the crowd
A T-shirt is launched from a height of 4 feet with an intal upward velocity of 72 feet per second
The T-shirt is caught 42 feet above the field
How long will take the T-shirt to reach its maximum height? What is the maximum height? What is the range of the function that models the height of the T-shirt over time?
2. During halftime of a football game, a sing shot launches T-shirts at the crowd
A T-shirt is launched from a height of 3 feet with an intal upward velocity of 80 feet per second
The T-shirt is caught 36 feet above the field
How long will take the T-shirt to reach its maximum height? What is the maximum height? What is the range of the function that models the height of the T-shirt over time?
Answers
Answer:
1. Using the kinematic equation h(t) = -16t^2 + v0t + h0, where h0 is the initial height, v0 is the initial velocity, and t is time, we have:
h(t) = -16t^2 + 72t + 4
To find the maximum height, we need to find the vertex of the parabolic function h(t). The t-coordinate of the vertex is given by t = -b/2a, where a = -16 and b = 72:
t = -b/2a = -72/(2(-16)) = 2.25 seconds
To find the maximum height, we substitute t = 2.25 seconds into the equation for h(t):
h(2.25) = -16(2.25)^2 + 72(2.25) + 4 = 82 feet
The range of the function h(t) is [4, 82], since the T-shirt starts at a height of 4 feet and reaches a maximum height of 82 feet before falling back to the ground.
2. Using the same kinematic equation as before, we have:
h(t) = -16t^2 + 80t + 3
To find the maximum height, we again need to find the vertex of the parabolic function h(t). The t-coordinate of the vertex is given by t = -b/2a, where a = -16 and b = 80:
t = -b/2a = -80/(2(-16)) = 2.5 seconds
To find the maximum height, we substitute t = 2.5 seconds into the equation for h(t):
h(2.5) = -16(2.5)^2 + 80(2.5) + 3 = 80 feet
The range of the function h(t) is [3, 80], since the T-shirt starts at a height of 3 feet and reaches a maximum height of 80 feet before falling back to the ground.
Step-by-step explanation:
In 2012, the population of a city was 5.51 million. The exponential growth rate was 3.82% per year.
a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
c) When will the population of the city be 10 million?
d) Find the doubling time.
helppppppp
Answers
Answer:
a) To find the exponential growth function, we can use the formula:
P(t) = P0 * e^(rt)
Where:
P(t) = the population at time t
P0 = the initial population (in this case, 5.51 million)
e = the mathematical constant e (approximately 2.71828)
r = the annual growth rate (in decimal form)
t = the number of years
Substituting the given values, we have:
P(t) = 5.51 * e^(0.0382t)
b) To estimate the population of the city in 2018, we can substitute t = 6 (since 2018 is 6 years after 2012) into the exponential growth function:
P(6) = 5.51 * e^(0.0382*6) ≈ 6.93 million
Therefore, the estimated population of the city in 2018 is approximately 6.93 million.
c) To find when the population of the city will be 10 million, we can set P(t) = 10 and solve for t:
10 = 5.51 * e^(0.0382t)
e^(0.0382t) = 10/5.51
0.0382t = ln(10/5.51)
t ≈ 11.7 years
Therefore, the population of the city will be 10 million in approximately 11.7 years from 2012, or around the year 2023.
d) To find the doubling time, we can use the formula:
T = ln(2) / r
Where:
T = the doubling time
ln = the natural logarithm
2 = the factor by which the population grows (i.e., doubling)
r = the annual growth rate (in decimal form)
Substituting the given value of r, we have:
T = ln(2) / 0.0382 ≈ 18.1 years
Therefore, the doubling time for the population of the city is approximately 18.1 years.
Which graph represents the hyperbola x2/52-y2/42 = 1?
Answers
For the given equation we have horizontal length of 5 and vertical width of 4 units. The graph that depicts this hyperbola is: Option B.
What is a hyperbola?A hyperbola is a particular kind of conic section in mathematics, which is a curve created by the intersection of a cone and a plane. The collection of all points in a plane that have a constant difference between them and two fixed points, known as the foci, is referred to as a hyperbola. The distance between the foci is referred to as this consistent difference and is represented by the symbol 2a.
Two separate branches that are mirror reflections of one another make up a hyperbola. The vertices are the two locations where the two branches of a hyperbola are joined.
For the given equation of the parabola, the value of a and b = 5 and 4.
Thus, we have horizontal length of 5 and vertical width of 4 units
The graph that depicts this hyperbola is: Option B.
Learn more about hyperbola here:
https://brainly.com/question/15697124
#SPJ1
The complete question is:
Given the expression 3x+2 evaluate the expression for the given values of x when x=(-2)
Answers
Answer:
...............................
The answer is -4.
Explanation:
First, plug the value of x in.
3(-2)+2
Then, multiply 3 and -2 since they are next to each other and order of operations PEMDAS tells you to multiply first.
-6+2
Lastly, add -6 and 2 to get -4.
Suppose that the function h is defined as follows.
if
-2
-1
h(x)= 0
1
2
Graph the function h.
-3.5
if-2.5
if-1.5
if -0.5
if 0.5 ≤x≤1.5
+
X
Ś
Answers
The required graph of the function given; h (x) has been attached.
Define a graph?In mathematics, graph theory is the study of graphs, which are mathematical structures used to represent pairwise interactions between objects. In this definition, a network is made up of nodes or points called vertices that are connected by edges, also called links or lines. In contrast to directed graphs, which have edges that connect two vertices asymmetrically, undirected graphs have edges that connect two vertices symmetrically. Graphs are one of the primary areas of study in discrete mathematics.
Here as per the question the graph of the function, h (x) has been attached.
To know more about graphs, visit:
brainly.com/question/17267403
#SPJ1
1. You go to the ice cream shop with your friends and you can choose an ice cream, a topping
and sprinkles. How many different sundaes can you make when you order one flavor of ice
cream, one topping and one color of sprinkles from the chart below? Show all possible
outcomes in a tree diagram.
Ice Cream
Chocolate
Vanilla
Strawberry
Topping
Fudge
Marshmallow
Sprinkles
Chocolate
Rainbow
a. How many sample spaces are there? HINT: How many possible combinations?
b. P (Chocolate, Fudge, Rainbow)
Answers
A. There are 9 sample spaces.
B. The probability of choosing Chocolate, Fudge, and Rainbow is 1/9
What is meant by sample spaces?
In probability theory, a sample space is the set of all possible outcomes of a random experiment or process. It is used to define the space of events and calculate probabilities.
What is meant by probability?
Probability is a measure of the likelihood of an event occurring, expressed as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. It is calculated by dividing the number of favourable outcomes by the total number of possible outcomes.
According to the given information
A. There are 9 possible combinations (3 ice cream flavors x 3 toppings x 1 sprinkle color), so there are 9 sample spaces.
B. The probability of choosing Chocolate, Fudge, and Rainbow is 1/9, assuming all combinations are equally likely.
To know more about probability visit
brainly.com/question/30034780
#SPJ1
Complete the truth table for (A ⋁ B) ⋀ ~(A ⋀ B).
Answers
The truth table for (A ⋁ B) ⋀ ~(A ⋀ B) is:
A B (A ⋁ B) ⋀ ~(A ⋀ B)
0 0 0
0 1 0
1 0 0
1 1 0
The truth table is what?A truth table is a table that displays all possible combinations of truth values (true or false) for one or more propositions or logical expressions, as well as the truth value of the resulting compound proposition or expression that is created by combining them using logical operators like AND, OR, NOT, IMPLIES, etc.
The columns of a truth table reflect the propositions or expressions themselves as well as the compound expressions created by applying logical operators to them. The rows of a truth table correspond to the various possible combinations of truth values for the propositions or expressions.
To complete the truth table for (A ⋁ B) ⋀ ~(A ⋀ B), we need to consider all possible combinations of truth values for A and B.
A B A ⋁ B A ⋀ B ~(A ⋀ B) (A ⋁ B) ⋀ ~(A ⋀ B)
0 0 0 0 1 0
0 1 1 0 1 0
1 0 1 0 1 0
1 1 1 1 0 0
So, the only case where the expression is true is when both A and B are true, and for all other cases it is false.
To know more about truth tables, visit:
https://brainly.com/question/31482105
#SPJ1
6. Two out of every five Canadians read at least 10 books a year. What percent of Canadians read at least 10 books a year?
Answers
40% of Canadians read at least 10 books a year.
Define percentageA percentage is a way of expressing a portion or a part of a whole as a fraction of 100. It is represented by the symbol "%". Percentages are often used to compare different quantities or to describe how much of a total is made up by a specific amount or group. For example, if you score 80 out of 100 on a test, your score can be expressed as 80%, meaning you got 80 out of 100 possible points.
If two out of every five Canadians read at least 10 books a year, then we can write this as a fraction:
2/5
We can multiply this fraction by 100 to turn it to a percentage:
(2/5) x 100 = 40%
Therefore, 40% of Canadians read at least 10 books a year.
To know more about fraction, visit:
https://brainly.com/question/10354322
#SPJ1
See the photo below
Answers
This problem involves integration and algebraic manipulation, and belongs to the subject of calculus. The solutions are:
[tex]A) $\int_{0}^{2} (f(x) + g(x)) dx = -3$[/tex]
[tex]B) $\int_{0}^{3} (f(x) - g(x)) dx = -4$[/tex]
[tex]C) $\int_{2}^{3} (3f(x) + g(x)) dx = -32$[/tex]
What is the explanation for the above response?
This is a problem that asks us to find the values of some definite integrals using given values of other definite integrals. We are given three definite integrals, and we are asked to compute three other integrals involving the same functions, using the given values.
The problem involves some algebraic manipulation and the use of the linearity of the integral.
It also involves finding the constant "a" that makes a definite integral equal to zero. The integral involves two functions, "f(x)" and "g(x)," whose definite integrals over certain intervals are also given.
See the attached for the full solution.
Learn more about integration at:
https://brainly.com/question/18125359
#SPJ1
2. Mrs. Cooper created a triangular shaped vegetable garden and needs to put down fertilizer to cover the space. If the garden has a base of 8m and a height of 10m, how much fertilizer will she need?
Answers
Answer:
40 m²
Step-by-step explanation:
Area of triangle:
To find the area of triangle, multiply the base and area and then divide it by 2.
base = b = 8 m
height = h = 10m
[tex]\boxed{\bf Area \ of \ triangle = \dfrac{1}{2}*b*h}[/tex]
[tex]= \dfrac{1}{2}*8 * 10\\\\= 4 * 10\\\\= 40 \ m^2[/tex]
Write an equation in point-slope form. Part I: Create an equation of a line in point-slope form. Be sure to identify all parts of the equation before writing the equation. (3 points) Part II: Using the equation of the line you wrote in Part I, write an equation of a line that is perpendicular to this line. Show your work. (3 points)
Answers
The line's equation in point-slope form is shown here. Point (2, 5) is the given point on the line, and slope 2 is the given slope of the line. The slope of this line is -1/2, which is the negative reciprocal of the slope.
How do you formulate an equation in point-slope form?A line's point slope form equation is [tex]y - y_1 = m(x - x_1)[/tex]. Consequently, y - 0 = m(x = 0), or y = mx, is the equation of a line passing through the origin with a slope of m.
We require a point on the line and the slope of the line in order to create a line equation in point-slope form. In point-slope form,
[tex]y - y1 = m(x - x1)[/tex]
As an illustration, suppose we want to formulate the equation of the line passing through the coordinates (2, 5) and having a slope of 2. The values can be entered into the point-slope form as follows:
y - 5 = 2(x - 2)Let's say the given line has the equation [tex]y - y1 = m(x - x1)[/tex], where (x1, y1) is a point on the line and m is the slope of the line.
we can use the given point (2, 5). Then we can plug in the values into the point-slope form:
[tex]y - 5 = (-1/2)(x - 2).[/tex]
To know more about point-slope visit:-
brainly.com/question/837699
#SPJ1
PLEASE HELP
Find the Area
2cm
___cm^2
Answers
Answer:
3.14 cm^2
Step-by-step explanation:
1. Find radius:
If diameter is 2, divide it by 2 to get radius = 1
2. Find formula:
A=πr^2
3. Plug in:
A = π(1)^2
4. Solve (multiply):
A = π(1)^2:
3.14159265359
Or
3.14 cm^2
Answer:
3.14 cm^2
Step-by-step explanation:
A=[tex]\pi[/tex]r^2
r=2
2/2=1
A=[tex]\pi[/tex](1)^2
=[tex]\pi[/tex]1
≈3.14x1
≈3.14cm^2
Which geometric term describes ∠ T A G ?
Answers
Answer:
angle
Step-by-step explanation:
since there is a < sign, that makes it an angle. I'm not sure if that is the whole problem, or if It is missing a picture. Hope this helps!
Answer: i know it is acute
You can afford a $1000 per month mortgage payment. You've found a 30 year loan at 5.3% interest.
a) How big of a loan can you afford? (Round to the nearest cent, as needed.)
$
b) How much total money will you pay the loan company? (Round to the nearest cent, as needed.)
$
c) How much of that money is interest? (Round to the nearest cent, as needed.)
Answers
Answer:
a) To find out how big of a loan you can afford, we can use the formula for the monthly payment of a mortgage:
M = P [ i(1 + i)^n ] / [ (1 + i)^n - 1 ]
where M is the monthly payment, P is the principal (the amount borrowed), i is the monthly interest rate (which is the annual interest rate divided by 12), and n is the number of monthly payments (which is the number of years times 12).
In this case, we know that M = $1,000, i = 0.053/12, and n = 30 x 12 = 360. We want to solve for P, the principal we can afford.
Substituting these values into the formula, we get:
$1,000 = P [ 0.004416(1 + 0.004416)^360 ] / [ (1 + 0.004416)^360 - 1 ]
Simplifying and solving for P, we get:
P = $183,928.72
Therefore, you can afford a loan of approximately $183,928.72.
b) The total money paid to the loan company will be the monthly payment multiplied by the number of payments over the life of the loan. In this case, we have:
Total money paid = $1,000 x 360 = $360,000
Therefore, the total amount of money paid to the loan company will be $360,000.
c) To find out how much of that money is interest, we can subtract the principal from the total amount paid. In this case, we have:
Interest paid = Total money paid - Principal = $360,000 - $183,928.72 = $176,071.28
Therefore, the amount of money paid in interest will be $176,071.28.
how am i supposed to prove that theyre collinear
Answers
Answer:
They are collinear if they are on the same line
Naya has a pitcher that contains 3 cups of salted lassi, a yogurt drink with sait and sites. She pours 6 fluid ounces of lassi into each glass. If she uses all of the lassi, how many glasses does Naya use?
A. 2
B. 4
C. 16
D. 18
Answers
After 6 fluid ounces , Naya uses 4 glasses as a result.
Define ounces?A unit of weight is an ounce. There are various kinds of ounces, including avoirdupois, troy, and fluid ounces. One sixteenth of a pound is equivalent to one avoirdupois ounce . A troy ounce, often known as an apothecaries' measure, is equivalent to 480 grains or one-twelfth of a pound. A volume unit is a fluid ounce. 1/8 of a cup, 2 tablespoons, or 6 teaspoons make to one fluid ounce
In Naya's pitcher, there are three glasses of salted lassi.
She fills each glass with six fluid ounces of lassi.
By translating cups to fluid ounces and dividing the entire amount of lassi by the amount put into each glass, we can determine how many glasses Naya uses if she consumes all of the lassi.
8 fluid ounces make constitute a cup.
Consequently, 3 cups equal 24 fluid ounces (3 x 8).
24 divided by 6 results in:
4 glasses are equal to 24/6.
Naya uses four glasses as a result.
To know more about ounces visit:
brainly.com/question/29374025
#SPJ1
ΔABC with vertices A(-3, 0), B(-2, 3), C(-1, 1) is rotated 180° clockwise about the origin. It is then reflected across the line y = -x. What are the coordinates of the vertices of the image?
A.
A'(0, 3), B'(2, 3), C'(1, 1)
B.
A'(0, -3), B'(3, -2), C'(1, -1)
C.
A'(-3, 0), B'(-3, 2), C'(-1, 1)
D.
A'(0, -3), B'(-2, -3), C'(-1, -1)
Answers
The coordinates of the vertices of the image is A'(0, -3), B'(3, -2), C'(1, -1). The correct option is B.
What are coordinates?Triangle ABC is rotated 180 degrees clockwise about the origin and then reflected across the line y=-x.
We are to find the coordinates of the vertices of the image.
We know that
if a point (x, y) is rotated 180 degrees clockwise, then its co-ordinate changes as follows :
(a, b) ⇒ (-a, -b).
So, after getting rotated 180 degrees clockwise, the coordinates of the vertices of triangle ABC becomes
A(-3, 0) ⇒ (3, 0)
B(-2, 3) ⇒ (2, -3)
C(-1, 1) ⇒ (1, -1).
Therefore, the correct option is B. A'(0, -3), B'(3, -2), C'(1, -1).
Learn more about coordinates, here:
https://brainly.com/question/5961156
#SPJ1
The monthly cost (in dollars) of a long-distance phone plan is a linear function of the total calling time (in minutes). The monthly cost for 35 minutes of calls is $16.83 and the monthly cost for 52 minutes is $18.87. What is the monthly cost for 39 minutes of calls?
Answers
Answer: We can use the two given points to find the equation of the line and then plug in 39 for the calling time to find the corresponding monthly cost.
Let x be the calling time (in minutes) and y be the monthly cost (in dollars). Then we have the following two points:
(x1, y1) = (35, 16.83)
(x2, y2) = (52, 18.87)
The slope of the line passing through these two points is:
m = (y2 - y1) / (x2 - x1) = (18.87 - 16.83) / (52 - 35) = 0.27
Using point-slope form with the first point, we get:
y - y1 = m(x - x1)
y - 16.83 = 0.27(x - 35)
Simplifying, we get:
y = 0.27x + 7.74
Therefore, the monthly cost for 39 minutes of calls is:
y = 0.27(39) + 7.74 = $18.21
Step-by-step explanation:
Please help me solve and show my work
Answers
The degree measure of the angles are;
1. 5π/3 = 300°
2 3π/4 = 135°
3. 5π/6 = 150°
4. -3π/2 = 90°
What is degree and radian?A degree is a unit of measurement which is used to measure circles, spheres, and angles while a radian is also a unit of measurement which is used to measure angles.
A circle has 360 degrees which are its full area while its radian is only half of it which is 180 degrees or one pi radian.
therefore π = 180°
1. 5π/ 3 = 5×180/3 = 300°
2. 3π/4 = 3× 180/4 = 540/4 = 135°
3. 5π/6 = 5×180/6 = 150°
4. - 3π/2 = -3 × 180/2 = -270° = 90°
learn more about degree and radian from
https://brainly.com/question/22689613
#SPJ1
LOOK AT THE PHOTO PLS
Answers
The next entry on the long division would be 0.054, and 0.0054
How to perform long divisionLong division is a method of dividing two numbers using a step-by-step process. Here's how to perform long division:
Step 1: Write the dividend (the number being divided) and the divisor (the number you're dividing by) in the long division format, with the dividend inside the division symbol and the divisor outside.
Read more on long division here:https://brainly.com/question/25289437
#SPJ1
solve the equation
a) y''-2y'-3y= e^4x
b) y''+y'-2y=3x*e^x
c) y"-9y'+20y=(x^2)*(e^4x)
Answers
Answer:
a) To solve the differential equation y''-2y'-3y= e^4x, we first find the characteristic equation:
r^2 - 2r - 3 = 0
Factoring, we get:
(r - 3)(r + 1) = 0
So the roots are r = 3 and r = -1.
The general solution to the homogeneous equation y'' - 2y' - 3y = 0 is:
y_h = c1e^3x + c2e^(-x)
To find the particular solution, we use the method of undetermined coefficients. Since e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = Ae^4x
Taking the first and second derivatives of y_p, we get:
y_p' = 4Ae^4x
y_p'' = 16Ae^4x
Substituting these into the original differential equation, we get:
16Ae^4x - 8Ae^4x - 3Ae^4x = e^4x
Simplifying, we get:
5Ae^4x = e^4x
So:
A = 1/5
Therefore, the particular solution is:
y_p = (1/5)*e^4x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^3x + c2e^(-x) + (1/5)*e^4x
b) To solve the differential equation y'' + y' - 2y = 3xe^x, we first find the characteristic equation:
r^2 + r - 2 = 0
Factoring, we get:
(r + 2)(r - 1) = 0
So the roots are r = -2 and r = 1.
The general solution to the homogeneous equation y'' + y' - 2y = 0 is:
y_h = c1e^(-2x) + c2e^x
To find the particular solution, we use the method of undetermined coefficients. Since 3xe^x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax + B)e^x
Taking the first and second derivatives of y_p, we get:
y_p' = Ae^x + (Ax + B)e^x
y_p'' = 2Ae^x + (Ax + B)e^x
Substituting these into the original differential equation, we get:
2Ae^x + (Ax + B)e^x + Ae^x + (Ax + B)e^x - 2(Ax + B)e^x = 3xe^x
Simplifying, we get:
3Ae^x = 3xe^x
So:
A = 1
Therefore, the particular solution is:
y_p = (x + B)e^x
Taking the derivative of y_p, we get:
y_p' = (x + 2 + B)e^x
Substituting back into the original differential equation, we get:
(x + 2 + B)e^x + (x + B)e^x - 2(x + B)e^x = 3xe^x
Simplifying, we get:
-xe^x - Be^x = 0
So:
B = -x
Therefore, the particular solution is:
y_p = xe^x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^(-2x) + c2e^x + xe^x
c) To solve the differential equation y" - 9y' + 20y = x^2*e^4x, we first find the characteristic equation:
r^2 - 9r + 20 = 0
Factoring, we get:
(r - 5)(r - 4) = 0
So the roots are r = 5 and r = 4.
The general solution to the homogeneous equation y" - 9y' + 20y = 0 is:
y_h = c1e^4x + c2e^5x
To find the particular solution, we use the method of undetermined coefficients. Since x^2*e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax^2 + Bx + C)e^4x
Taking the first and second derivatives of y_p, we get:
y_p' = (2Ax + B)e^4x + 4Axe^4x
y_p'' = 2Ae^4x +
Write an equation for the polynomial graphed below
Answers
The polynomial in factor form is y(x) = - (1 / 6) · (x + 3) · (x + 1) · (x - 2) · (x - 3).
How to derive the equation of the polynomial
In this problem we find a representation of polynomial set on Cartesian plane, whose expression is described by the following formula in factor form:
y(x) = a · (x - r₁) · (x - r₂) · (x - r₃) · (x - r₄)
Where:
x - Independent variable.r₁, r₂, r₃, r₄ - Roots of the polynomial.a - Lead coefficient.y(x) - Dependent variable.Then, by direct inspection we get the following information:
y(0) = - 3, r₁ = - 3, r₂ = - 1, r₃ = 2, r₄ = 3
First, determine the lead coefficient:
- 3 = a · (0 + 3) · (0 + 1) · (0 - 2) · (0 - 3)
- 3 = a · 3 · 1 · (- 2) · (- 3)
- 3 = 18 · a
a = - 1 / 6
Second, write the complete expression:
y(x) = - (1 / 6) · (x + 3) · (x + 1) · (x - 2) · (x - 3)
To learn more on polynomials: https://brainly.com/question/29260355
#SPJ1
14. The local credit union is offering a special student checking account. The monthly cost of the account is $15. The first 10 checks are free, and each additional check costs $0.75. You search
the Internet and find a bank that offers a student checking account with no monthly charge. The first 10 checks are free, but each additional check costs $2.50.
a. Assume that you will be writing more than 10 checks a month. Let n represent the number of checks written in a month. Write a function rule for the cost c of each account in terms of n.
b. Write an inequality to determine what number of checks in the bank account would be more expensive than the credit union account.
c. Solve the inequality in part b.
Answers
Answer: a. c(n) = 15 + 0.75(n - 10)
b. 15 + 0.75(n - 10) = 2.50(n - 10)=
Simplifying and solving for n, we get:
n = 50
c. n > 50
Step-by-step explanation:
a. The cost c of the credit union account in terms of the number of checks written n can be expressed as:
c(n) = 15 + 0.75(n - 10)
The first term, 15, represents the monthly cost of the account, and the second term represents the additional cost per check beyond the first 10 free checks.
The cost c of the bank account in terms of the number of checks written n can be expressed as:
c(n) = 2.50(n - 10)
The first term, 0, represents the monthly cost of the account, and the second term represents the additional cost per check beyond the first 10 free checks.
b. We want to find the number of checks for which the bank account is more expensive than the credit union account. Let x be the number of checks that makes the cost of the two accounts equal. Then we have:
15 + 0.75(n - 10) = 2.50(n - 10)
Simplifying and solving for n, we get:
n = 50
So if the number of checks written in a month is greater than 50, the bank account will be more expensive than the credit union account.
c. The solution to the inequality is:
n > 50
This means that the number of checks written in a month must be greater than 50 for the bank account to be more expensive than the credit union account.
Given that sin 0 = 20/29 and that angle terminates in quadrant III, then what is the value of tan 0?
Answers
The value of Tanθ is 20/21.
What is Pythagorean Theorem?
A right triangle's three sides are related in Euclidean geometry by the Pythagorean theorem, also known as Pythagoras' theorem. According to this statement, the areas of the squares on the other two sides add up to the size of the square whose side is the hypotenuse.
Here, we have
Given: sinθ = -20/29 and that angle terminates in quadrant III.
We have to find the value of tanθ.
Using the definition of sine to find the known sides of the unit circle right triangle. The quadrant determines the sign on each of the values.
Sinθ = Perpendicular/hypotenuse
Find the adjacent side of the unit circle triangle. Since the hypotenuse and opposite sides are known, use the Pythagorean theorem to find the remaining side.
Adjacent = - √Hypotenuse² - perpenducualr²
Replace the known values in the equation.
Adjacent = -√29² - (-20)²
Adjacent = -21
Find the value of tangent.
Tanθ = Perpendicular/base
Tanθ = -20/(-21)
Hence, the value of Tanθ is 20/21.
To learn more about the Pythagorean Theorem from the given link
https://brainly.com/question/28981380
#SPJ1
What is the mean of the values in the stem-and-leaf plot?
Enter your answer in the box.
Answers
Answer:
mean = 24
Step-by-step explanation:
the mean is calculated as
mean = [tex]\frac{sum}{count}[/tex]
the sum of the data set is
sum = 12 + 13 + 15 + 28 + 28 + 30 + 42 = 168
there is a count of 7 in the data set , then
mean = [tex]\frac{168}{7}[/tex] = 24
Primary Level 2 3 4 5 6 7. 8 children/funny monkeys thin/rake strong/ox eagle/aeroplane my room/ clean/ whistle swimmer/fish Exercise 2 Read the story. Look for the simile (as/like) When Mr. Bumble is angry, he shouts as loud as thunder. His eyes look like fire. He bangs his hands which feel as heavy as lead. Mr. Bumble stamps his feet like an et All the pupils keep as quiet as lambs when Mr. Bumble behaves like e
Answers
The similes in the story are:
"shouts as loud as thunder""eyes look like fire""hands feel as heavy as lead""stamps his feet like an et""quiet as lambs"What is a Simile?A simile is a figure of speech that compares two things using the words "like" or "as." It is a type of metaphor that helps to create a vivid and engaging image in the reader or listener's mind.
Similes are often used in literature, poetry, and everyday language to make a comparison more relatable and understandable. For example, "He is as brave as a lion" or "She sings like an angel." These similes help to convey a certain quality or trait by comparing it to something else that is well-known or familiar.
Note: It seems there may be a typo in the last sentence of the story, where the word "e" appears instead of "elephant" or another word that would make sense in context.
Read more about similes here:
https://brainly.com/question/2416704
#SPJ1
The diameter of a circle is 38 feet.what is the circles circumfrence. Use 3.14 for pi
Answers
Answer:
The circumference of the circle is 119.32 ft.
Step-by-step explanation:
The circumference of a circle can be solved through the formula:
C = πd
where d is the diameter
Given: d = 38 ft
π = 3.14
Solve:
C = πd
C = 3.14 (38 ft)
C = 119.32 ft
Oliver and Mike each place some apples and oranges into the same bowl.
• The ratio of apples to oranges Oliver places in the bowl is 2:3
• The ratio of apples to oranges Mike places in the bowl is 1:2
• They each place 6 oranges in the bowl.
Write the total number of apples and oranges they place in the bowl.
Answers
Answer: 5 * 5 = 20
20 divided by 1 = 20
If there are 5 apples with an apple:orange ratio of 1:4, there are 20 oranges.