Answers
Answer
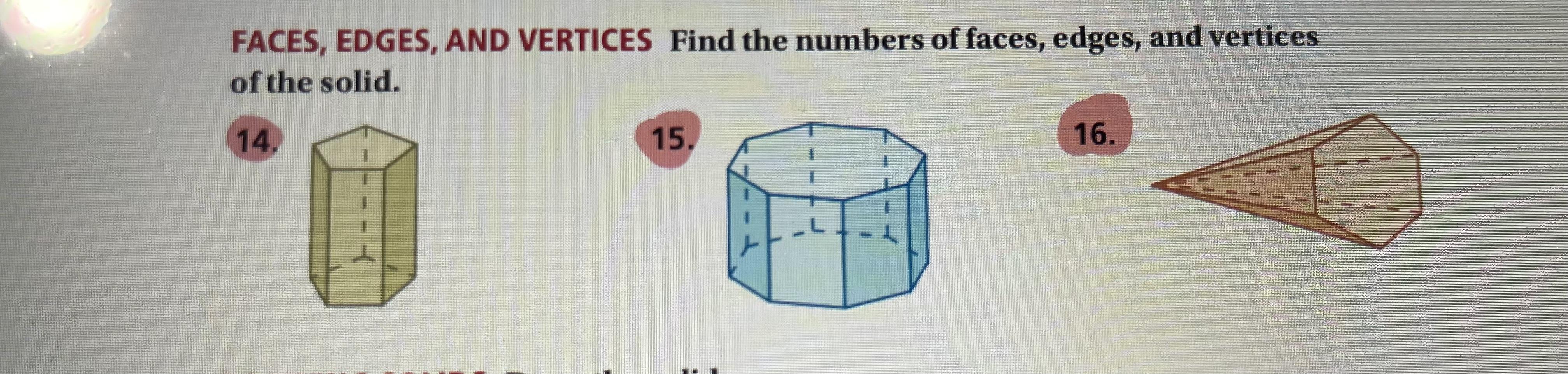
Number 14: 7 faces, 15 edges, and 10 vertices.
Number 15: 10 faces, 24 edges, and 16 vertices.
Number 16: 7 faces, 12 edges, and 7 vertices.
:D
Step-by-step explanation:
Related Questions
Find the volume of a pyramid with a square base, where the area of the base is 19. 6 ft 2 19. 6 ft 2 and the height of the pyramid is 11. 6 ft 11. 6 ft. Round your answer to the nearest tenth of a cubic foot
Answers
If the area of the base is 19. 6 ft^2 and the height of the pyramid is 11. 6 ft, the volume of the pyramid is approximately 79.1 cubic feet.
The formula for the volume of a pyramid is given by:
V = (1/3) × base area × height
In this case, we are given that the pyramid has a square base, so the base area is simply the area of a square with side length s:
base area = s^2 = 19.6 ft^2
We are also given the height of the pyramid:
height = 11.6 ft
Substituting these values into the formula for the volume of a pyramid, we get:
V = (1/3) × base area × height
= (1/3) × 19.6 ft^2 × 11.6 ft
≈ 79.1 ft^3 (rounded to the nearest tenth)
To learn more about volume click on,
https://brainly.com/question/23861754
#SPJ4
The function:
V(x) = x(10-2x)(16-2x), 0
a) Find the extreme values of V.
b) Interpret any valuse found in part (a) in terms of volumeof the box.
Answers
The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.
To find the extreme values of V, we need to take the derivative of V and set it equal to zero. So, let's begin:
[tex]V(x) = x(10-2x)(16-2x)[/tex]
Taking the derivative with respect to x:
[tex]V'(x) = 10x - 4x^2 - 32x + 12x^2 + 320 - 48x[/tex]
Setting V'(x) = 0 and solving for x:
[tex]10x - 4x^2 - 32x + 12x^2 + 320 - 48x = 0\\8x^2 - 30x + 320 = 0[/tex]
Solving for x using the quadratic formula:
[tex]x = (30 ± \sqrt{(30^2 - 4(8)(320))) / (2(8))\\x = (30 ± \sqrt{(1680)) / 16\\x = 0.93 or x =5.07[/tex]
So, the extreme values of V occur at x ≈ 0.93 and x ≈ 5.07. To determine whether these are maximum or minimum values, we need to examine the second derivative of V. If the second derivative is positive, then the function has a minimum at that point. If the second derivative is negative, then the function has a maximum at that point. If the second derivative is zero, then we need to use a different method to determine whether it's a maximum or minimum.
Taking the second derivative of V:
V''(x) = 10 - 8x - 24x + 24x + 96
V''(x) = -8x + 106
Plugging in x = 0.93 and x = 5.07:
V''(0.93) ≈ 98.36 > 0, so V has a minimum at x ≈ 0.93.
V''(5.07) ≈ -56.56 < 0, so V has a maximum at x ≈ 5.07.
Now, to interpret these values in terms of the volume of the box, we need to remember that V(x) represents the volume of a box with length 2x, width 2x, and height x. So, the maximum value of V occurs at x ≈ 5.07, which means that the volume of the box is greatest when the height is about 5.07 units. The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.
learn more about extreme values
https://brainly.com/question/1286349
#SPJ11
a) The extreme values of V are:
Minimum value: V(0) = 0
Relative maximum value: V(3) = 216
Absolute maximum value: V(4) = 128
b) The absolute maximum value of V at x = 4 represents the case where the box has a square base of side length 4 units, height 2 units, and width 8 units, which has a volume of 128 cubic units.
a) To find the extreme values of V, we first need to find the critical points of the function. This means we need to find where the derivative of the function equals zero or is undefined.
Taking the derivative of V(x), we get:
[tex]V'(x) = 48x - 36x^2 - 4x^3[/tex]
Setting this equal to zero and solving for x, we get:
[tex]48x - 36x^2 - 4x^3 = 0[/tex]
4x(4-x)(3-x) = 0
So the critical points are x = 0, x = 4, and x = 3.
We now need to test these critical points to see which ones correspond to maximum or minimum values of V.
We can use the second derivative test to do this. Taking the derivative of V'(x), we get:
[tex]V''(x) = 48 - 72x - 12x^2[/tex]
Plugging in the critical points, we get:
V''(0) = 48 > 0 (so x = 0 corresponds to a minimum value of V)
V''(4) = -48 < 0 (so x = 4 corresponds to a maximum value of V)
V''(3) = 0 (so we need to do further testing to see what this critical point corresponds to)
To test the critical point x = 3, we can simply plug it into V(x) and compare it to the values at x = 0 and x = 4:
V(0) = 0
V(3) = 216
V(4) = 128
So x = 3 corresponds to a relative maximum value of V.
b) In terms of the volume of the box, the function V(x) represents the volume of a rectangular box with a square base of side length x and height (10-2x) and width (16-2x).
The minimum value of V at x = 0 represents the case where the box has no dimensions (i.e. it's a point), so the volume is zero.
The relative maximum value of V at x = 3 represents the case where the box is a cube with side length 3 units, which has a volume of 216 cubic units.
for such more question on extreme values
https://brainly.com/question/30886356
#SPJ11
these four geometry questions i’m not quite sure how to do and have been struggling in them for a while and it’s due tomorrow!!!!
Answers
The total areas of each composite shape are:
1) 121 in²
2) 150m²
3) 14.03 ft²
4) 538.36 cm²
How to find the area of the composite figure?1) Formula for area of a rectangle is:
Area = Length * width
Thus:
Area of composite shape = (9 * 8) + (7 * 7)
= 121 in²
2) Formula for area of rectangle is:
Area = Length * width
Area = 12 * 5 = 60 m²
Area of triangle = ¹/₂ * base * height
Area = ¹/₂ * 12 * 15
Area = 90 m²
Area of composite shape = 60 + 90 = 150m²
3) Area of triangle = ¹/₂ * 3 * 7 = 10.5 ft²
Area of semi circle = ¹/₂ * πr²
= ¹/₂ * π * 1.5²
= 3.53 ft²
Total composite area = 10.5 ft² + 3.53 ft²
Total composite area = 14.03 ft²
4) Total composite area = (¹/₂ * π * 7.5²) + (30 * 15)
= 538.36 cm²
Read more about Area of composite figure at: https://brainly.com/question/10254615
#SPJ1
From a horizontal distance of 80.0 m, the angle to the top of a flagpole is 18°. Calculate the height of the flagpole to the nearest tenth of a meter.
1. 24.7 meters
2. 76.1 meters
3. 26.0 meters
4. 25.3 meters
Answers
Answer:
The figure is omitted--please sketch it to confirm my answer.
Set your calculator to degree mode.
Let h be the height of the flagpole.
[tex] \tan(18) = \frac{h}{80} [/tex]
[tex]h = 80 \tan(18) = 25.994[/tex]
The height of the flagpole is approximately 26.0 meters. #3 is correct.
Solve the following problem. Be sure to show all the steps (V. E. S. T. ) and work in order to receive full credit.
The sum of three numbers is 26. The second number is twice the first and the third number is 6 more than the second. Find the numbers.
Please help due tomorrow
Answers
The three numbers are 4, 8, and 14.
Let's use variables to represent the three numbers
Let x be the first number.
Then the second number is twice the first, so it is 2x.
The third number is 6 more than the second, so it is 2x + 6.
We know that the sum of the three numbers is 26, so we can write an equation:
x + 2x + (2x + 6) = 26
Now we can solve for x
5x + 6 = 26
5x = 20
x = 4
So the first number is 4.
To find the second number, we can use the equation we wrote earlier:
2x = 2(4) = 8
So the second number is 8.
To find the third number, we can use the other equation we wrote earlier
2x + 6 = 2(4) + 6 = 14
So the third number is 14.
Learn more about equation here
brainly.com/question/14603452
#SPJ4
three machines, a, b, c produce a large number of identical products. 60% of the products come from machine a, 30% from b and 10% from c. historical records indicate that 10% of the parts produced by machine a are defective, compared with 30% for machine b and 40% for machine c. what is the probability that a randomly chosen part is defective?
Answers
The probability that a randomly chosen part is defective is 0.16, or 16%.
The probability that a randomly chosen part is defective, we need to use the law of total probability.
Let [tex]$D$[/tex] be the event that a part is defective and let [tex]$M_i$[/tex] be the event that the part came from machine [tex]$i$[/tex], for [tex]$i = A, B, C$[/tex].
Then we have:
[tex]$P(D) = P(D|M_A)P(M_A) + P(D|M_B)P(M_B) + P(D|M_C)P(M_C)$[/tex]
60% of the products come from machine A, 30% from machine B, and 10% from machine C.
Therefore:
[tex]$P(M_A) = 0.6$[/tex]
[tex]$P(M_B) = 0.3$[/tex]
[tex]$P(M_C) = 0.1$[/tex]
The probability of a part being defective is 10% if it comes from machine A, 30% if it comes from machine B, and 40% if it comes from machine C.
Therefore:
[tex]$P(D|M_A) = 0.1$[/tex]
[tex]$P(D|M_B) = 0.3$[/tex]
[tex]$P(D|M_C) = 0.4$[/tex]
Substituting these values into the law of total probability, we get:
[tex]$P(D) = 0.1 \cdot 0.6 + 0.3 \cdot 0.3 + 0.4 \cdot 0.1 = 0.16$[/tex]
For similar questions on randomly
https://brainly.com/question/24140969
#SPJ11
Which statement is true?
Please help
Answers
Ans-6
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups. She writes the equation r = 2/5 to describe the relationship.
Answers
In the given equation r = 2/5 t "r" is the dependent variable.
Dependent variables:In mathematics, a variable is a symbol that represents a quantity that can take on different values. In many cases, variables can be divided into two types: dependent variables and independent variables.
An independent variable is a variable that can be changed freely, and its value is not dependent on any other variable in the equation.
A dependent variable is a variable whose value depends on the value of one or more other variables in the equation
Here we have
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups.
She writes the equation r = 2/5 t to describe the relationship.
In the equation, r = 2/5 t, "t" represents the total number of cups, while "r" represents the number of cups of red paint.
Here "t" is the independent variable because it represents the total number of cups, which can be changed arbitrarily.
The value of "r" depends on the value of "t" because the number of cups of red paint is always 2/5 of the total number of cups.
Therefore,
In the given equation r = 2/5 t "r" is the dependent variable.
Learn more about Variables at
https://brainly.com/question/1479694
#SPJ1
Complete Question:
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups. She writes the equation r = 2/5 t to describe the relationship. Which is the independent variable? Which is the dependent variable? Explain how you know.
An angle measures 37.6° more than the measure of its complementary angle. What is the measure of each angle?
Answers
The pair of required complementary angles are 26.2° and 63.8° respectively.
What are complementary angles?Two angles are said to be supplementary angles because they combine to generate a linear angle when their sum is 180 degrees.
When two angles add up to 90 degrees, however, they are said to be complimentary angles and together they make a right angle.
If the total of two angles is 90o (ninety degrees), then the angles are complementary.
A 30-angle and a 60-angle, for instance, are two complementary angles.
So, to find the 2 angles which are complementary:
x + x + 37.6 = 90
Now, solve it as follows:
x + x + 37.6 = 90
2x = 90 - 37.6
2x = 52.4
x = 52.4/2
x = 26.2
Now, x = 26.2 and the second angle x + 37.6 is = 26.2 + 37.6 = 63.8°.
Therefore, the pair of required complementary angles are 26.2° and 63.8° respectively.
Know more about complementary angles here:
https://brainly.com/question/16281260
#SPJ1
call a positive integer kinda-prime if it has a prime number of positive integer divisors. if there are $168$ prime numbers less than $1000$, how many kinda-prime positive integers are there less than $1000$?
Answers
There are 173 kinda-prime positive integer less than 1000.
To find the number of kinda-prime positive integer less than 1000, we'll follow these steps:
1. Understand the definition of a kinda-prime number: A positive integer is kinda-prime if it has a prime number of positive integer divisors.
2. Determine the number of prime numbers less than 1000: There are 168 prime numbers less than 1000, as given.
3. Determine the possible prime number of divisors: Since 168 is not too large, we only need to consider 2 and 3 as possible prime numbers of divisors for a kinda-prime number.
4. Analyze the cases:
Case 1: Kinda-prime numbers with 2 divisors (prime numbers)
All prime numbers have exactly 2 divisors (1 and itself). Thus, all 168 prime numbers less than 1000 are kinda-prime.
Case 2: Kinda-prime numbers with 3 divisors
Let N be a kinda-prime number with 3 divisors. Then, N = p^2 for some prime number p. To find the suitable prime numbers p, we need[tex]p^2 < 1000[/tex]. The prime numbers that meet this condition are 2, 3, 5, 7, and 11 (since 13^2 = 169 > 1000). Therefore, there are 5 additional kinda-prime numbers ([tex]2^2, 3^2, 5^2, 7^2, and 11^2[/tex]).
5. Add the total number of kinda-prime numbers from both cases: 168 + 5 = 173.
Learn more about integer here:
https://brainly.com/question/17118150
#SPJ11
[tex]$(\pi(1000)-1)+11=\boxed{177}$[/tex] "kind a-prime" positive integers less than $1000$.
Let [tex]$n$[/tex] be a positive integer with[tex]$k$[/tex] positive integer divisors.
If [tex]$k$[/tex] is prime, then.
[tex]$n$[/tex] is a "kind a-prime" integer.
[tex]$k$[/tex] must be of the form.
[tex]$k=p$[/tex] or [tex]$k=p^2$[/tex] for some prime [tex]$p$[/tex].
If [tex]$k=p$[/tex], then [tex]$n$[/tex] must be of the form.
[tex]$p^{p-1}$[/tex] for some prime [tex]$p$[/tex]. Since [tex]$p < 1000$[/tex], there are.
[tex]$\pi(1000)$[/tex]possible values of [tex]$p$[/tex].
[tex]$p=2$[/tex] gives [tex]$2^1$[/tex], which is not prime, so we have to subtract.
[tex]$1$[/tex] from [tex]$\pi(1000)$[/tex] to get the number of possible.
[tex]$p$[/tex].
[tex]$\pi(1000)-1$[/tex] values of [tex]$p$[/tex] that give a "kind a-prime" integer of this form.
If [tex]$k=p^2$[/tex], then [tex]$n$[/tex] must be of the form.
[tex]$p^{p^2-1}$[/tex] for some prime[tex]$p$[/tex].
There are.
[tex]$\pi(31)=11$[/tex] primes less than [tex]$31$[/tex], and each of them gives a different "kind a-prime" integer of this form.
Since [tex]$31^5 > 1000$[/tex], no primes larger than [tex]$31$[/tex]can be used to form a "kind a-prime" integer of this form.
[tex]$11$[/tex] possible values of [tex]$p$[/tex] that give a "kind a-prime" integer of this form.
For similar questions on Positive Integer
https://brainly.com/question/16952898
#SPJ11
Which property was used to simplify the expression? 3c+ 9 + 4c = 3c + 4c + 9
Answers
The property used to simplify the expression is the Commutative Property of Addition, which states that changing the order of addends does not change the sum.
What is Commutative Property?The Commutative Property is a property of operations that states that the order in which two numbers are added or multiplied does not affect the result. In other words, the property says that changing the order of the terms being added or multiplied will not change the final answer.
According to given information:The property that was used to simplify the expression is the Commutative Property of Addition. This property states that the order in which we add two numbers does not affect the result. In other words, if we have two numbers a and b, then a + b is equal to b + a.
In the given expression, we have two terms, 3c and 4c, that are being added together. By applying the Commutative Property of Addition, we can rearrange the terms to get 4c + 3c. This gives us the simplified expression 7c + 9.
To know more about Commutative Property visit:
https://brainly.com/question/778086
#SPJ1
. imagine you had a research question in which you wanted to compare a sample mean to the mean of a population. under these circumstances you would either do a z-test or a one-sample t-test. what key piece of information would be missing if you needed to do a one-sample t-test?
Answers
Sample size and sample standard deviation are the key information needed for a single-sample t-test.
In the event that you need to compare the test cruel with the populace cruel, and you perform a single-sample t-test rather than a z-test, the vital piece of data that will be lost is the populace standard deviation.
Within the z-test, the populace standard deviation is known and the standard mistake of the cruel is calculated utilizing the populace standard deviation.
In a single-sample t-test, the populace standard deviation is obscure, and the standard mistake of the cruel is evaluated from the test standard deviation.
Therefore, sample size and sample standard deviation are the key information needed for a single-sample t-test.
learn more about standard deviation
brainly.com/question/23907081
#SPJ4
6 greater than a number is 24.
Answers
Answer:
Step-by-step explanation:
6 greater than a number is 24.
This means adding 6 to a number, x, will equal 24.
6 + x = 24
subtract 6 from both sides of the equation, and you are left with x=18
18 is your answer!!
if p is a prime number and a is a positive inte- ger, how many distinct positive divisors does pa have?
Answers
If p is a prime number and a is a positive integer, then pa has (a+1) distinct positive divisors.
A prime number is a positive integer greater than 1, which is divisible only by 1 and itself. Divisors are the numbers that evenly divide a given number.
For a prime number p raised to the power of a (p^a), the number of distinct positive divisors can be found using the following formula:
Number of divisors = (a + 1)
This is because each power of p from 0 to a can divide p^a without any remainder, giving us a total of a + 1 distinct divisors. These divisors are:
1, p, p^2, p^3, ..., p^(a-1), p^a
For example, if p = 2 (a prime number) and a = 3 (a positive integer), then the number of distinct positive divisors for 2^3 (which is 8) would be:
Number of divisors = (3 + 1) = 4
The divisors for 2^3 (8) are 1, 2, 4, and 8.
Learn more about Prime numbers here: brainly.com/question/30358834
#SPJ11
For the first half of a baseball season, a player had 90 hits out of 270 times at bat. The player's batting average was
90
270
≈ 0. 333. During the second half of the season, the player had 64 hits out of 276 times at bat. The player's batting average was
64
276
≈ 0. 232. (Round your answers to three decimal places. )
(a) What is the average (mean) of 0. 333 and 0. 232?
Answers
The issue inquires to discover the normal (cruel) of two values:
0.333 and 0.232. To do this, able to essentially include the two values together and partition them by 2. Including the two values gives us:
0.333 + 0.232 = 0.565
Separating by 2 gives us:
0.565 / 2 = 0.2825
So the normal of 0.333 and 0.232 is 0.2825.
In any case, the issue inquires to circular our answer to three decimal places, which suggests we have to be circular 0.2825 to the closest thousandth. The third decimal put maybe a 2, which implies we circular down. Hence, the ultimate reply is roughly 0.283, adjusted to three decimal places.
To learn about partition visit:
https://brainly.com/question/30191477
#SPJ4
As a nurse working in a hospital one of the jobs is to give appropriate doses of medicine
before surgery so the patient doesn't wake up during surgery. 4cc of this particular medicine is
meant for a 180lb man, what would be the correct dosage for a 145 lb. woman?
Answers
Answer:
the correct dosage of the medicine for a 145 lb. woman would be approximately 3.22 cc
Step-by-step explanation:
To calculate the correct dosage of the medicine for a 145 lb. woman, we can use the following formula:
dosage = (weight of patient / weight of reference patient) x reference dosage
where the weight of the reference patient is 180 lb. and the reference dosage is 4 cc.
Plugging in the given values, we get:
dosage = (145 / 180) x 4
= 3.22 cc (rounded to two decimal places)
Therefore, the correct dosage of the medicine for a 145 lb. woman would be approximately 3.22 cc. However, it's important to note that dosages of medications should only be determined by a qualified medical professional based on a number of factors, including the patient's weight, medical history, and current condition.
If r=0.5 m, A = ???
(Use the r key.)
Answers
The calculated value of the angular velocity of the object is 2 rad/s.
Calculating the angular velocityThe angular velocity, denoted by the Greek letter omega (ω), represents the rate of change of the angle with respect to time.
For an object moving in a circular path, the angular velocity is related to the linear speed and the radius of the circle by the equation:
ω = v/r
where v is the linear speed and r is the radius.
In this case, the radius is 0.5m and the speed is 1ms−1. Thus, the angular velocity is:
ω = v/r = 1/0.5 = 2 radians per second (rad/s)
Therefore, the angular velocity of the object is 2 rad/s.
Read more about angular velocity at
https://brainly.com/question/9408577
#SPJ1
Complete question
An object moves in a circular path of radius 0.5m with a speed of 1ms−1. What is its angular velocity (A)?
If r = 0.5 m, A = ???
Evaluate the expression when x = 7 (4x + 9) - 4(x - 1) + x use the answer choices in the diagram
Answers
Answer:
The answer is 20
Step-by-step explanation:
when x=7
(4x+9)-4(x-1)+x
(4(7)+9)-4(7-1)+7
28+9 -4(6)+7
37+7-24
44-24
=20
the weights of newborn baby boys born at a local hospital are believed to have a normal distribution with a mean weight of 3245 grams and a standard deviation of 625 grams. if a newborn baby boy born at the local hospital is randomly selected, find the probability that the weight will be greater than 2620 grams. round your answer to four decimal places.
Answers
The probability that the weight of a randomly selected newborn baby boy born at the local hospital will be greater than 2620 grams is 0.9099 (rounded to four decimal places).
The probability can be calculated using the standard normal distribution as follows:
P(Z > (2620 - 3245) / 625) = P(Z > -1.335)
Using a standard normal distribution table, we find that the probability of Z being greater than -1.335 is 0.9099.
We use the standard normal distribution because we know the mean and standard deviation of the population of newborn baby boys' weights. We convert the raw score of 2620 grams to a z-score, which tells us how many standard deviations the raw score is away from the mean.
Learn more about probability
https://brainly.com/question/24756209
#SPJ4
in a recent basketball game, shenille attempted only three-point shots and two-point shots. she was successful on 20% of her three-point shots and 30% of her two-point shots. shenille attempted 30 shots. how many points did she score?(2013 amc 12a
Answers
The probability of a score for a recent basketball game, shenille attempted only three-point shots and two-point shots is 18 points in the game. The answer is Option B.
Let x be the number of three-point shots and y be the number of two-point shots attempted by Shenille.
Then, we have:
x + y = 30 (total number of shots attempted)
Let's solve for one of the variables. For example, we can solve for x by subtracting y from both sides of the equation:
x = 30 - y
Now, we can express Shenille's points in terms of x and y:
Points = 3x + 2y
Substituting x = 30 - y, we get:
Points = 3(30 - y) + 2y
Points = 90 - y
Shenille's success rate for three-point shots is 20%, so the number of successful three-point shots she made is 0.2x. Similarly, the number of successful two-point shots she made is 0.3y.
Total points scored = (0.2x)(3) + (0.3y)(2)
Substituting x = 30 - y, we get:
Total points scored = (0.2(30 - y))(3) + (0.3y)(2
Total points scored = 18 + 0.4y
Now we need to maximize the total points scored by Shenille. Since she attempted 30 shots in total, we have:
y = 30 - x
Substituting this into the equation for total points, we get:
Total points scored = 18 + 0.4(30 - x)
Total points scored = 30 - 0.4x
This is a linear function, which is maximized at its endpoint. The maximum value of this function occurs at x = 0, which means Shenille attempted all two-point shots. In this case, y = 30, and the total points scored would be:
Total points scored = 0 + 0.3(30)(2)
Total points scored = 18
Learn more about probability at
https://brainly.com/question/30034780
#SPJ4
The question is -
In a recent basketball game, Shenille attempted only three-point shots and two-point shots. She was successful on 20% of her three-point shots and 30% of her two-point shots. Shenille attempted 30 shots. How many points did she score?
(A) 12
(B) 18
(C) 24
(D) 30
(E) 36
Lucia has three separate pieces of ribbon. Each piece is 5 yards long. She needs to cut pieces that are 27 inches long to decorate folklorico dance dresses. What is the greatest number of 27-inch pieces that she can cut from three pieces of ribbon?
A 20
B 18
C 7
D 6
Answers
The greatest number of 27-inch pieces that she can cut from three pieces of ribbon is found to be 19. So, option B is the correct answer choice.
Each yard is equal to 36 inches, so 5 yards are equal to 180 inches. Therefore, each piece of ribbon is 180 inches long.
To find out how many 27-inch pieces Lucia can cut from each piece of ribbon, we divide 180 by 27.
180/27 = 6.67
Since Lucia can only cut whole pieces, she can cut 6 pieces of ribbon from each piece of ribbon.
Therefore, she can cut a total of 6 x 3 = 18 pieces of ribbon from the three separate pieces of ribbon.
Learn more about Division :
https://brainly.com/question/19871608
#SPJ4
Given the following code fragment, which of the following expressions is always true?
int x;
scanf("%d", &x);
A) if( x = 1)
B) if( x < 3)
C) if( x == 1)
D) if((x/3) > 1)
Answers
If the expressions given, only C) if( x == 1) is always true.
In the given code fragment, the value of x is read from the user using the scanf() function. The value of x can be any integer value, depending on what the user enters. After the value of x is read, the program checks the value of x using a conditional statement (if statement) and executes the code inside the if statement only if the condition is true.
Expression A) if( x = 1) assigns the value 1 to x and then checks if x is true. This means that the condition is always true, because the assignment operation (=) returns the assigned value (in this case, 1), which is a non-zero value and therefore considered true in C programming.
Expression B) if( x < 3) checks if x is less than 3. This expression is not always true, as x can be any value greater than or equal to 3, in which case the condition would be false.
Expression C) if( x == 1) checks if x is equal to 1. This expression is always true if the user enters the value 1 for x.
Expression D) if((x/3) > 1) checks if the integer division of x by 3 is greater than 1. This expression is not always true, as x can be any value less than or equal to 3, in which case the result of the integer division by 3 would be 1 or less, in which case the condition would be false.
Learn more about expressions
https://brainly.com/question/14083225
#SPJ4
the only expression that is always true in this code fragment is option C) if( x == 1).
The expression that is always true in this code fragment is option C) if( x == 1).
Option A) if( x = 1) is not always true because it is an assignment statement instead of a comparison statement. It assigns the value 1 to x instead of checking if x is equal to 1.
Option B) if( x < 3) is also not always true because x could be any number less than 3.
Option D) if((x/3) > 1) is not always true because x could be any number less than or equal to 3, in which case the expression would evaluate to false.
Therefore, the only expression that is always true in this code fragment is option C) if( x == 1).
learn more about code fragment
https://brainly.com/question/31133611
#SPJ11
If you spin the spinner 36 times, what is the best prediction possible for the number of times
it will land on green or blue?
Answers
The best prediction possible for the number of times the spinner will land on green or blue is given as follows:
30 spins.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
Out of six regions, three are green and two are blue, hence the probability of one spin resulting in green or blue is given as follows:
p = (3 + 2)/6
p = 5/6.
Thus the expected number out of 36 trials of spins resulting in green or blue is given as follows:
E(X) = 5/6 x 36
E(X) = 30 spins.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
A rectangular plece of paper with length 28 cm and width 14 cm has two semicircles cut out of it, as shown below. Find the area of the paper that remains. Use the value 3.14 for 1, and do not round your answer. G ✓6 14 cm 0 00 H cm X 2023 McGraw Hill LLC As Rights Reserve
Answers
The area of the paper remains is 238.14 cm².
What is area?Area is the region bounded by a plane shape.
To calculate the area of the paper that remains, we use the formula below.
Formula:
Area of the paper that remains(A) = Area of the rectangle(LW)-Area of the two semi circles [π(W/2)²]A = LW- [π(W/2)²]................ Equation 1Where:
L = Length of the rectangleW = Width of the rectangle = Diameter of the semi circleFrom the diagram in the question,
Given:
L = 28 cmW = 14 cmSubstitute these values into equation 1
A = (28×14)-[3.14(14/2)²A = 392-153.86A = 238.14 cm²Hence, the area is 238.14 cm².
Learn more about area here: https://brainly.com/question/28470545
#SPJ1
You need to lower your debt to credit limit ratio by $1000. Your current limit is $1400. $1000 is what percent of your credit limit
Answers
$1000 is 71.43 percent of the credit limit.
To lower the debt to credit limit ratio by $1000, you have a few options. The first option is to increase your credit limit by requesting a higher limit from your credit card issuer. Alternatively, you can pay off some of your outstanding balance to reduce your debt. Either way, it's important to make sure you're not maxing out your credit limit, as this can negatively impact your credit score.
It's also a good idea to review your spending habits and create a budget to ensure you're not overspending and accumulating debt. By making responsible financial decisions and managing your credit wisely, you can improve your credit score and achieve your financial goals.
To calculate the percentage of $1000 in terms of the credit limit of $1400, we need to divide $1000 by $1400 and multiply the result by 100. This gives us,
($1000 / $1400) x 100 = 71.43%
Therefore, $1000 is approximately 71.43% of the credit limit of $1400.
To learn more about percent here:
https://brainly.com/question/30704720
#SPJ4
HELP PLS EXPLAIN THISSSSS
Answers
Plugging in the values given into the expression, and simplifying, we would have our answer as: B. [tex]\frac{9}{25}[/tex]
How to Evaluate an Expression?To evaluate an expression, follow these steps:Identify the variables and constants in the expression.Substitute the given values for each variable in the expression.Simplify the expression until there are no more operations left.Given that, a = 5 and k = -2, substitute the values into the expression given and simplify:
[tex](\frac{3^2(5^{-2})}{3(5^{-1})} )^{-2}[/tex]
Simplify:
[tex](\frac{9 * \frac{1}{25} }{3* \frac{1}{5} } )^{-2}[/tex]
[tex](\frac{\frac{9}{25} }{\frac{3}{5} } )^{-2}\\\\(\frac{9}{25} * \frac{5}{3} } )^{-2}\\\\(\frac{3}{5} )^{-2}\\\\ = \frac{9}{25}[/tex]
Learn more about value of an expression on:
https://brainly.com/question/625174
#SPJ1
What is the slope of the line?
-2
-1
1
2
Answers
Answer: positive 2
Step-by-step explanation:
The data for the height and weight of different people was collected the line of best fit for this date it was determined to be Y equals 0. 9 1X -65. 5 where X is the height in centimeters and why is the weight in kilograms is in the equation predict the height of a person who weighs 63 kg
Answers
According to the equation, a person who weighs 63 kg is predicted to be approximately 141 centimeters tall.
The equation given is Y = 0.91X - 65.5, where X represents the height in centimeters and Y represents the weight in kilograms. To predict the height of a person who weighs 63 kg, we need to solve for X, the height in centimeters.
To do this, we can plug in the given weight of 63 kg for Y in the equation and then solve for X. So, we have:
63 = 0.91X - 65.5
Adding 65.5 to both sides, we get:
63 + 65.5 = 0.91X
Simplifying, we have:
128.5 = 0.91X
Finally, to solve for X, we divide both sides by 0.91, giving:
X = 141.21
To know more about equation here
https://brainly.com/question/10413253
#SPJ4
in a study of the treatment of congestive heart failure (chf), a new surgical procedure was compared to the standard surgical procedure. the study enrolled 550 people with chf and randomly assigned half to receive the new procedure and half to receive the standard procedure. among those that received the new procedure, 98 died within 5 years. among those that received the standard procedure, 190 died within 5 years. what is the result for the appropriate measure to describe the strength of the association between surgical procedure and death?
Answers
The result for the appropriate measure, relative risk, is approximately 0.515.
This indicates that the risk of death within 5 years is about 51.5% lower in the new procedure group compared to the standard procedure group.
This suggests a strong association between the surgical procedure and the reduction in the risk of death.
To determine the strength of the association between the surgical procedures and death, we can calculate the relative risk.
Identify the numbers given in the question.
- Total participants: 550
- New procedure group: 275 (half of 550)
- Deaths in new procedure group: 98
- Standard procedure group: 275 (half of 550)
- Deaths in standard procedure group: 190
Calculate the death rate (proportion of deaths) in each group.
- Death rate in new procedure group = (Number of deaths in new procedure group) / (Total in new procedure group) = 98/275 ≈ 0.356
- Death rate in standard procedure group = (Number of deaths in standard procedure group) / (Total in standard procedure group) = 190/275 ≈ 0.691
Calculate the relative risk.
- Relative risk = (Death rate in new procedure group) / (Death rate in standard procedure group) = 0.356/0.691 ≈ 0.515.
For similar question on standard.
https://brainly.com/question/187506
#SPJ11
You select a marble without looking and then put it back. If you do this 24 times, what is the
best prediction possible for the number of times you will pick a marble that is not orange?
times
Answers
Step-by-step explanation:
24 times, as there are no orange marbles in the set.
so, every pull will produce a marble that is not orange with 100% certainty.
in general, we have 12 marbles.
let's change the problem description into picking a marbles that is not blue.
we have 6 blue marbles.
the chance to pick a blue marble is therefore 6/12 = 1/2.
and the probability to not pick a blue marbles is 1 - 1/2 = 1/2.
so, in 24 pulls, we expect 24× 1/2 = 12 times to get a marble that is not blue.
or change it to "not green" marbles.
5 green marbles.
the probability to pick a green marble is 5/12.
the probabilty to not pick a green marble = 1 - 5/12 = 7/12.
in 24 pulls we expect 24 × 7/12 = 14 times to get a marble that is not green.
it change it to "not purple" marbles.
1 purple marble.
the probability to pick a purple marble is 1/12.
the probabilty to not pick a purple marble = 1 - 1/12 = 11/12.
in 24 pulls we expect 24 × 11/12 = 22 times to get a marble that is not purple.