Answers
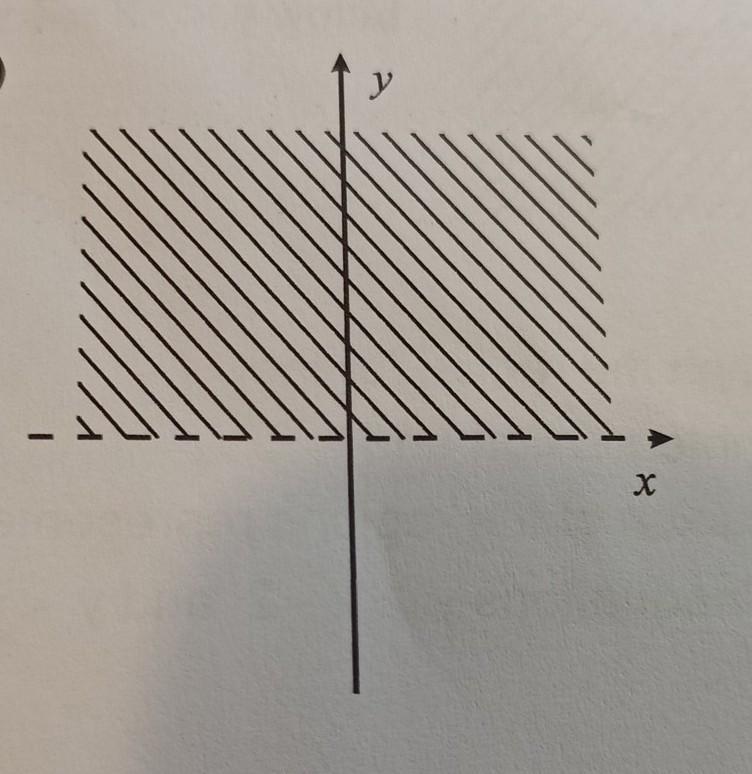
The inequality expression representing the area of the shaded region, indicating both the shaded area and the broken line is; y > 0
What is an inequality?An inequality is a mathematical statement consisting two expressions joined with inequality symbols, which includes; '<', '>', '≠', '≤', and '≥'.
The area of the shaded region is the part of the coordinate plane above the x-axis.
The region shaded can therefore be indicated by the area y > 0
The x-axis on the coordinate plane representing the boundary of the shaded region consists of broken line, which indicates that the line is not included in the shaded region.
The inequality representing the area of the shaded region is therefore;
y > 0
Learn more on writing inequalities here: https://brainly.com/question/21575354
#SPJ1
Related Questions
a man can hit his target 25% of the time if he fires 4 shots in succession what is the probability that he will hit his target
Answers
The probability that the man will hit his target at least once in 4 shots is calculated using the complementary probability of him missing all 4 shots. Since he hits his target 25% of the time, he misses it 75% of the time.
The probability of missing all 4 shots is (0.75)^4 = 0.3164.
Now, to find the probability of hitting the target at least once, subtract the probability of missing all shots from 1:
1 - 0.3164 = 0.6836 or 68.36%.
So, the probability that the man will hit his target at least once in 4 shots is approximately 68.36%.
Learn more about probability:
https://brainly.com/question/24756209
#SPJ11
HELP ME PLEASE!!!!!!!
Answers
Answer:
Step-by-step explanation:
Graph # Matching equation
1 |-3x|
2 |-x|
3 -|2x|
You can tell which one matches by finding the slope and whether the V points up or down
The length of one leg of a right triangle is 2 times the length of the other, and the
length of the hypotenuse is 12. What is the length of the longest leg?
Answers
Answer:
[tex]\frac{24\sqrt{5} }{5}[/tex]
Step-by-step explanation:
Let's start by assigning one of the unknown legs with the variable x.
We know that the other leg is 2 times the length of x, so we can write:
2x
We also know that the length of the hypotenuse is 12.
From here, we can use the Pythagorean Theorem.
Recall that the Pythagorean Theorem is:
[tex]a^2+b^2=c^2[/tex]
where a is the length of one leg, b is the length of the other leg, and c is the length of the hypotenuse.
Let's substitute the values. We have:
[tex]x^2+(2x^2)=12^2=\\x^2+4x^2=144=\\5x^2=144=\\x^2=\frac{144}{5}=\\x=\frac{12}{\sqrt{5} }[/tex]
Let's rationalize the denominator by multiplying the numerator and denominator by [tex]\sqrt{5}[/tex], like so:
[tex]\frac{12}{\sqrt{5} } =\\\frac{12\sqrt{5} }{5}[/tex]
Therefore, [tex]x=\frac{12\sqrt{5} }{5}[/tex]
Let's solve for 2x:
[tex]2x=\\2(\frac{12\sqrt{5} }{5})=\\ \frac{24\sqrt{5} }{5}[/tex]
So, the length of the longest leg is [tex]\frac{24\sqrt{5} }{5}[/tex]
what is the probability that a student will complete the exam in more than 60 minutes but less than 75 minutes? (round your answer to four decimal places.)
Answers
The Probability that a student will complete the exam 0.2676.
The probability of completing the exam in one hour or less is:
[tex]P (x < 60)[/tex]
= [tex]P (z < (60-83)/13)[/tex]
=[tex]P (z < -1.77)[/tex]
= 0.0384.
The probability that a student will complete the exam in more than 60 minutes, but less than 75 minutes is.
[tex]P (60 < x < 75)[/tex]
= [tex]P (x < 75)-P (x < 60)[/tex]
Now,
[tex]P (x < 75)[/tex]
=[tex]P (z < (75-83)/13)[/tex]
= [tex]P (z < -0.62)[/tex]
=0.2676.
For similar question on Probability
https://brainly.com/question/13604758
#SPJ11
Can please someone help me ASAP? It’s due tomorrow. I will give brainliest if it’s all correct!!
Please do part a, b, and c
Answers
The sample space are:
{AR, AS, AT, AE, RA, RS, RT, RE, SA, SR, ST, SE, TA, TR, TS, TE, EA, ER, ES, ET}
The favorable outcomes care:
{RS, RT, SR, ST, TR, TS}
The probability is 0.3 or 30%
How to find the sample spacePart A:
The sample space represents all possible outcomes that can occur when two cards are randomly selected without replacement from the given pile of cards.
The sample space can be represented as follows:
{AR, AS, AT, AE, RA, RS, RT, RE, SA, SR, ST, SE, TA, TR, TS, TE, EA, ER, ES, ET}
Part B:
The favorable outcomes are those outcomes in which both cards are consonants. In this case, the consonants are R, S, and T.
The favorable outcomes can be represented as follows:
{RS, RT, SR, ST, TR, TS}
Part C:
To calculate the probability of selecting 2 cards that are consonants, we need to find the ratio of favorable outcomes to the sample space.
The number of favorable outcomes is 6, and the size of the sample space is 20.
Therefore, the probability of selecting 2 cards that are consonants is:
P(consonants) = favorable outcomes / sample space
P(consonants) = 6 / 20
P(consonants) = 0.3 or 30%
Learn more about sample space at
https://brainly.com/question/10558496
#SPJ1
Please help offering 15 points
Answers
More people that rode the roller coaster are between the ages of 11 and 30, than people that are between the ages of 41 and 60 is the best description of the data which is obtained by using the arithmetic operations.
What are arithmetic operations?
Any real number may be explained using the four basic operations, also referred to as "arithmetic operations." Operations like division, multiplication, addition, and subtraction come before operations like quotient, product, sum, and difference in mathematics.
We are given a chart. From the chart we get the following data:
Number of people aged 11 - 20 riding roller coaster = 20
Number of people aged 21 - 30 riding roller coaster = 15
Number of people aged 31 - 40 riding roller coaster = 10
Number of people aged 41 - 50 riding roller coaster = 5
Number of people aged 51 - 60 riding roller coaster = 0
Using addition operation, we get
Total people = 20 + 15 + 10 + 5 + 0
Total people = 40
Now,
Total riders between 11 - 30 = 20 + 15
Total riders between 11 - 30 = 35
Similarly,
Total riders between 41 - 60 = 5 + 0
Total riders between 41 - 60 = 5
Hence, the fourth option is the correct answer.
Learn more about arithmetic operations from the given link
brainly.com/question/30283549
#SPJ1
scenic cinemas surveyed its audience and found that while most movie goers prefer weekends, seniors visit on weekdays. how should the theatre respond?
Answers
Scenic Cinemas should offer discounted weekday matinee showings for seniors and continue to focus on weekend showings for their broader audience.
How should Cinemas tailor their offerings to accommodate both preferences?Based on the survey results, it would be wise for Scenic Cinemas to tailor their offerings to accommodate both preferences.
One option would be to offer discounted weekday matinee showings targeted toward seniors. This could incentivize them to visit on weekdays while also offering them a more affordable option. At the same time, Scenic Cinemas could continue to focus on weekend showings to cater to their broader audience.
Another approach would be to offer more diverse programming during the weekdays, such as classic films or independent movies that may appeal more to seniors. This could create a niche for Scenic Cinemas and attract a more loyal customer base.
Ultimately, it's important for Scenic Cinemas to balance the needs of their different audience segments to maximize revenue and customer satisfaction. By offering targeted promotions and programming, they can ensure that both seniors and other moviegoers feel valued and have a reason to visit the theatre.
Learn more about survey trends
brainly.com/question/29751975
#SPJ11
ASAP Please help me do a two column proof for this. I am struggling
Answers
∠A = ∠C in trapezoid ABCD with arcAB = arcCD, can be proven with the property of isosceles triangles.
How to prove the relation?Since arcAB = arcCD, the lengths of the two arcs are equal. This implies that the lengths of the segments subtended by these arcs, AB and CD, are also equal.
Let E and F be the midpoints of the non-parallel sides AD and BC, respectively. Connect E and F with a line segment EF.
Since E and F are midpoints, DE = EA and BF = FC. In addition, since AB = CD = L, we can say that:
DE + EA = BF + FC
EA = FC
So, by the Hypotenuse-Leg (HL) theorem of congruence, triangles AEF and CFE are congruent:
ΔAEF ≅ ΔCFE
Now, since the triangles are congruent, their corresponding angles are equal:
∠A = ∠C
Find out more on trapezoids at https://brainly.com/question/26303997
#SPJ1
Please only do 9,11, and 13! And please help!! 40 points!!!
Answers
9. The volume of the triangular pyramid is given by:
V = (1/3)Bh
Here, B is the base area.
The base is shaped as a right triangle thus, using the Pythagoras Theorem we have:
h = sqrt(26.7² - 11.7²) = 23.274 km
The area if the base is:
B = (1/2)bh = (1/2)(11.7 km)(23.4 km) = 136.89 sq. km
Now, the volume is:
V = (1/3)(136.89)(15) = 2053.35 cubic km
Hence, the volume of the triangular pyramid is 2053.35 cubic km.
9. The volume of the triangular pyramid is 2053.35 cubic km. 11. The area of the shaded portion is 348.19 cubic in 13. The slant height of the cone is 8.53 meters.
What is Pythagoras Theorem?A fundamental conclusion in geometry relating to the lengths of a right triangle's sides is known as Pythagoras' theorem. According to the theorem, the square of the length of the hypotenuse, the side that faces the right angle, in any right triangle, equals the sum of the squares of the lengths of the other two sides, known as the legs.
9. The volume of the triangular pyramid is given by:
V = (1/3)Bh
Here, B is the base area.
The base is shaped as a right triangle thus, using the Pythagoras Theorem we have:
h = √(26.7² - 11.7²) = 23.274 km
The area if the base is:
B = (1/2)bh = (1/2)(11.7 km)(23.4 km) = 136.89 sq. km
Now, the volume is:
V = (1/3)(136.89)(15) = 2053.35 cubic km
Hence, the volume of the triangular pyramid is 2053.35 cubic km.
11. The volume of a cone is given by:
V = (1/3)πr²h
The dimension of the bigger cone is radius is 9 in, and height 15 in:
V1 = (1/3)π(9 in)²(15 in) = 381.7 cubic in
The dimension of the smaller cone is radius is 4 in, and height 10 in:
V2 = (1/3)π(4 in)²(10 in) = 33.51 cubic in
Now, the area of the shaded portion is:
V1 - V2 = 381.7 - 33.51 = 348.19
13. The volume of a cone is given by:
V = (1/3)πr²h
Substituting the values we have:
542.87 = (1/3)π(6 m)²h
h = 542.87 / [(1/3)π(6 m)²] = 6.05 m
Now, using the Pythagoras Theorem for the slant height we have:
s² = r² + h²
s² = (6 m)² + (6.05 m)²
s² = 72.9
s = √(72.9) = 8.53 m
The slant height of the cone is 8.53 meters.
Learn more about Pythagoras Theorem here:
https://brainly.com/question/21926466
#SPJ1
Solve the IVP given by y''+y=t, y(0)=1, y'(0)=-2
Answers
The solution to the IVP given by y''+y=t, y(0)=1, y'(0)=-2 is y(t) = cos(t) - (3/2) sin(t) + (1/2) t.
To solve the Initial Value Problem, we can use the method of undetermined coefficients, which involves assuming a particular form for the solution to the non-homogeneous equation y'' + y = t, and then finding the coefficients of the terms in that form by substituting it back into the equation.
First, we find the general solution to the homogeneous equation y'' + y = 0
The characteristic equation is r² + 1 = 0, which has solutions r = ±i. Therefore, the general solution to the homogeneous equation is
y_h(t) = c₁ cos(t) + c₂ sin(t),
where c₁ and c₂ are constants determined by the initial conditions.
Next, we assume a particular form for the non-homogeneous solution, based on the form of the right-hand side t. Since t is a linear function, we assume that the particular solution has the form
y_p(t) = a t + b.
Substituting this into the differential equation, we get
y''_p + y_p = t
2a + (at+b) = t.
Equating coefficients, we get
a = 1/2, b = 0.
Therefore, the particular solution is
y_p(t) = (1/2) t.
The general solution to the non-homogeneous equation is then the sum of the homogeneous and particular solutions
y(t) = y_h(t) + y_p(t)
= c₁ cos(t) + c₂ sin(t) + (1/2) t.
To determine the constants c₁ and c₂, we use the initial conditions:
y(0) = c₁ cos(0) + c₂ sin(0) + (1/2) (0) = c₁ = 1,
y'(0) = -c₁ sin(0) + c₂ cos(0) + (1/2) (1) = c₂ - (1/2) = -2,
so c₂ = -3/2.
Therefore, the solution to the IVP is
y(t) = cos(t) - (3/2) sin(t) + (1/2) t.
Learn more about Initial Value Problem here
brainly.com/question/30547172
#SPJ4
is $60 a resonable tax for a purchase of $120 what likey caused herschel to make the mistake
Answers
X and y represent positive integers such that 18x+11y= 2020. What is the greatest possible value of x+y
Answers
Answer:
To find the greatest possible value of x + y, we need to maximize the values of x and y such that they are still positive integers and satisfy the given equation 18x + 11y = 2020.
We can start by rearranging the equation to solve for y:
11y = 2020 - 18x
y = (2020 - 18x)/11
For y to be a positive integer, 2020 - 18x must be divisible by 11. We can test values of x starting from x = 1 and increasing by 1 until we find the largest possible value of x that satisfies this condition.
When x = 1, 2020 - 18x = 2002, which is divisible by 11. This gives us a value of y = 182/11, which is not a positive integer.
When x = 2, 2020 - 18x = 1984, which is divisible by 11. This gives us a value of y = 180/11, which is not a positive integer.
When x = 3, 2020 - 18x = 1966, which is divisible by 11. This gives us a value of y = 178/11, which is not a positive integer.
When x = 4, 2020 - 18x = 1948, which is divisible by 11. This gives us a value of y = 176/11, which is not a positive integer.
When x = 5, 2020 - 18x = 1930, which is divisible by 11. This gives us a value of y = 174/11, which is not a positive integer.
When x = 6, 2020 - 18x = 1912, which is divisible by 11. This gives us a value of y = 172/11, which is not a positive integer.
When x = 7, 2020 - 18x = 1894, which is divisible by 11. This gives us a value of y = 170/11, which is not a positive integer.
When x = 8, 2020 - 18x = 1876, which is divisible by 11. This gives us a value of y = 168/11, which is not a positive integer.
When x = 9, 2020 - 18x = 1858, which is divisible by 11. This gives us a value of y = 166/11, which is not a positive integer.
When x = 10, 2020 - 18x = 1840, which is divisible by 11. This gives us a value of y = 164/11, which is not a positive integer.
When x = 11, 2020 - 18x = 1822, which is divisible by 11. This gives us a value of y = 162/11, which is not a positive integer.
When x = 12, 2020 - 18x = 1804, which is divisible by 11. This gives us a value of y = 160/11, which is not a positive integer.
When x = 13, 2020 - 18x = 1786, which is divisible by 11. This gives us a value of y = 158/11, which is not a positive integer.
When x = 14, 2020 - 18x = 1768, which is divisible by 11. This gives us a value of y = 156/11, which is not a positive integer.
When x = 15, 2020 - 18x = 1750, which is divisible by 11. This gives us a value of y = 154/11, which is not a positive integer.
When x = 16, 2020 - 18x = 1732, which is divisible by 11. This gives us a value of y = 152/11, which is not a positive integer.
When x = 17, 2020 - 18x = 1714, which is divisible by 11. This gives us a value of y = 150/11, which is not a positive integer.
When x = 18, 2020 - 18x = 1696, which is divisible by 11. This gives us a value of y = 148/11, which is not a positive integer.
When x = 19, 2020 - 18x = 1678, which is divisible by 11. This gives us a value of y = 146/11, which is not a positive integer.
When x = 20, 2020 - 18x = 1660, which is divisible by 11. This gives us a value of y = 144
Ms. Yamato's gross pay is $2644. Her deductions total $548.30.
What percent of her gross pay is take-home pay?
A. 84%
B. 79%
C. 21%
D. 18%
Answers
Thus, the correct Percent response is B) 79%.
what is a percent?Percentage refers to a portion of every hundred. Although the abbreviations "pct.", "pct.", and occasionally "pc" are also used, it is frequently shown using the percent sign, "%".
If you have 100 apples and distribute 10 of them, for instance, you have distributed 10% of your total apple supply.
We deduct Ms. Yamato's deductions from her gross income to determine her take-home pay:
$2644 - $548.30 = $2095.702.
By dividing her take-home pay by her gross pay and multiplying the result by 100%, we can determine what proportion of her gross pay is taken home:
($2095.70 / $2644) * 100% = 79%
Thus, the correct response is B) 79%.
To know more about percent visit:
brainly.com/question/28670903
#SPJ1
A factory has two assembly lines, M and N, that make the same toy. On Monday, only assembly line M was functioning and it made 900 toys.
On Tuesday, both assembly lines were functioning for the same amount of time. Line M made 300 toys per hour and line N made 480 toys per hour. Line N made as many toys on Tuesday as line M did over both days.
Write an equation that can be used to find the number of hours, t, that the assembly lines were functioning on Tuesday.
Answers
Answer: First choice 480t = 300t + 900
Step-by-step explanation:
A factory has two assembly lines, M and N, that make the same toy. On Monday, only assembly line M was functioning and it made 900 toys.
On Tuesday, both assembly lines were functioning for the same amount of time. Line M made 300 toys per hour and line N made 480 toys per hour. Line N made as many toys on Tuesday as line M did over both days.
Write an equation that can be used to find the number of hours, t, that the assembly lines were functioning on Tuesday.
ANS
Let say t is time in hrs for Which Both Assembly line worked
M made 300 toys per hr on Tuesday
Toys made on Tuesday at Assembly line M = 300 × t = 300t toys
N made 480 toys per hr on Tuesday
Toys made on Tuesday at Assembly line N = 480 × t = 480t toys
Toys Made by N on Tuesday = Toys made by M on Tuesday + Toys made by M on Monday
480t = 300t + 900
=> 180 t = 900
=> t = 900/180
=> t = 5 hr
N capacity on tuesday Per hour * t = M capacity on tuesday per hour * t + Toys made by M on Monday
N = N capacity on tuesday Per hour
M = M capacity on tuesday Per hour
=> t (N - M ) = 900
=> t = 900/(N-M)
PLS HURRY!!
The length of ribbons found at a seamstress are listed. 3, 6, 9, 11, 12, 13 What is the appropriate measure of variability for the data shown, and what is its value?
Answers
Thus, the appropriate measure of variability found for the given data is 10.
Explain about the range of the data:The difference here between maximum and smallest values in a data set is known as the range. Utilizing the exact same units as the data, it measures variability. More variability is shown by larger values.
The range in statistics refers to the distribution of your data between the lowest and greatest value in the distribution. It is a widely used indicator of variation. Measures of variability provide you with descriptive statistics for summarising your data set in addition to measurements of central tendency.Given length of ribbons:
3, 6, 9, 11, 12, 13
Minimum value = 3
Maximum value = 13
Actually, the range, which is determined by deducting the lowest value from the greatest value in the dataset, would be the proper measure of variability for this data.
Range = Maximum value - Minimum value
Range = 13 - 3
Range = 10
Thus, the appropriate measure of variability found for the given data is 10.
Know more about the range of the data:
https://brainly.com/question/24326172
#SPJ1
Please help me with this homework
Answers
Answer: Circumference = 18 π cm
Step-by-step explanation:
We can use this formula to find the circumference of a circle:
➜ r is equal to the radius, also known as half the width of a circle.
C = 2πr
We will substitute our known values and solve for C by multiplying. Since the answer option includes π in our units, we do not multiply this into the 18.
C = 2πr
C = 2π(9)
C = 18 π cm
Answer: 18π
Step-by-step explanation:
The circumference of a circle is equal to 2πr, with r being equal to the radius. The radius of a circle is defined as the length from any point on the circle to its middlemost point. In this case, we are given the value of the radius as defined by the line. The radius equals 9, which we can plug into the equation.
C= 2πr
C = 2π(9)
C = 18π = 56.55
Hope this helps!
2)
Phillip has 8 red balls, 3 green balls, 6 yellow balls, 3 orange balls, 13 black balls
and 15 blue balls in his bag.
Mean: | 0,2, Median :
Mode:
Range
Answers
The results of the balls in Phillip's bag are:
The mean = 8.
The median = 7.
The mode = blue
The range = 12
How do we calculate the Mean, Median, Mode and Range?The mean (or the average) is the sum of all the values divided by the total number of values. Let's calculate the mean for the given data:
Total number of balls = 8 + 3 + 6 + 3 + 13 + 15 = 48
Mean = (8 + 3 + 6 + 3 + 13 + 15) / 6 = 48 / 6 = 8
Mean = 8.
The median is the middle value when a set of values is arranged in ascending or descending order.
Let's arrange the given data in ascending:
3, 3, 6, 8, 13, 15
As the total number of values is even, the median will be the average of the two middle values, which are 6 and 8.
Median = (6 + 8) / 2 = 7
The median = 7.
The mode is the value that appears most frequently in a set of values. Let's find the mode of the given data:
Red balls: 8
Green balls: 3
Yellow balls: 6
Orange balls: 3
Black balls: 13
Blue balls: 15
Blue balls have the highest frequency (i.e., 15) among all the colors.
The range is the difference between the highest and lowest values in a set of values. Let's find the range of the given data:
Highest value = 15 (blue balls)
Lowest value = 3 (green balls and orange balls)
Range = Highest value - Lowest value = 15 - 3 = 12
Range = 12.
Learn more about the mean at brainly.com/question/1136789
#SPJ1
Please use Triangle Inequality to solve, I'm having a bit of trouble. I'd also appreciate if you just help me.
Answers
The value of x for the given triangle through which the perimeter of the given relation is satisfied is 10.
What about perimeter of triangle?
The perimeter of a triangle is the total length of its boundary, which is the sum of the lengths of its three sides. The perimeter can be thought of as the distance around the triangle, and it is measured in units of length such as centimeters, meters, or feet. The perimeter of a triangle is an important geometric property that is used in many practical applications, such as calculating the amount of fencing needed to enclose a triangular-shaped garden or determining the length of wire required to form a triangular circuit.
According to the given information:
The perimeter of triangle is sum of all sides of the triangle
In which,
2x + 4 + 3x - 8 + x - 2 = 54
6x - 6 = 54
6x = 60
x = 10
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
a bacteria culture starts with 40 bacteria and grows at a rate proportional to its size. after 2 hours there are 180 bacteria. find the number of bacteria after 5 hours.
Answers
The number of bacteria after 5 hours is approximately 1013.8.
We can use the formula for exponential growth to solve this problem. If a population grows at a rate proportional to its size, then we can writ
N(t) = N₀ × e^(rt),
where N(t) is the size of the population at time t, N₀ is the initial size of the population, r is the growth rate, and e is the mathematical constant approximately equal to 2.71828.
We know that the culture starts with 40 bacteria, so N₀ = 40. We also know that after 2 hours, the size of the population is 180. We can use this information to solve for r:
180 = 40 × e^(2r)
180/40 = e^(2r)
ln(180/40) = 2r
r = ln(180/40)/2
r ≈ 0.6931
Now we can use the formula to find the size of the population after 5 hours:
N(5) = 40 × e^(0.6931×5)
N(5) ≈ 1013.8
Learn more about exponential growth here
brainly.com/question/12490064
#SPJ4
At a computer manufacturing company, they produce two different types of computers. They can make 70 laptops per day while making 55 desktops per day. The company has a total of 14 machines to make computers. They can make a total of 905 computers per day. How many machines make laptops and how many make desktops?
Write a system of equations and solve.
Answers
Answer:
Yo wassup bro, at this computer factory, they be making two types of computers, laptops and desktops. They churn out 70 laptops a day and 55 desktops a day. They got a total of 14 machines to make these computers. And they make a total of 905 computers a day. We gotta figure out how many machines are making laptops and how many are making desktops, ya know?
Alright, let's set up a system of equations to solve this. Let's call the number of machines making laptops "x" and the number of machines making desktops "y".
So, we got two equations here:
The total number of computers they make in a day is 905, so we can write: x laptops + y desktops = 905.
They got a total of 14 machines, so we can write: x + y = 14.
Now, let's solve this system of equations to find the values of x and y, man. Once we got those, we'll know how many machines are making laptops and how many are making desktops at this computer factory, yo!
data from a sample of randomly selected students is shown below. the variables collected are: exercise - the number of hours a student exercise per week debt - the amount of student loan debt (in thousands of dollars) a student is expected to graduate with age - the age of a student gpa - the gpa of a student descriptive statistics exercise debt age gpa n 241 196 254 248 lo 95% ci 7.0769 8.8655 20.069 3.2702 mean 7.8133 11.311 20.500 3.3200 up 95% ci 8.5497 13.757 20.931 3.3822 sd 5.8032 17.361 3.5000 0.3400 minimum 0.0000 0.0000 17.000 1.7500 1st quartile 4.0000 0.0000 19.000 3.0200 median 7.0000 3.0000 20.000 3.3600 3rd quartile 10.000 20.000 21.000 3.6950 maximum 35.000 100.00 41.000 4.0000 someone claims that the mean exercise time of all students is 10 hours per week. how would you respond? group of answer choices at the 95% confidence level, the mean exercise time of all students might be 10 hours per week. i am 95% confident that the mean exercise time of all students equals 7.8133 hours per week. i am 95% confident that the mean exercise time of all students is greater than 10 hours per week. i am 95% confident that the mean exercise time of all students is less than 10 hours per week.
Answers
The most appropriate response to the claim would be: "At the 95% confidence level, the mean exercise time of all students might not be 10 hours per week based on the sample data."
How do you 95% confident about the claim?Based on the given data, we can see that the sample mean exercise time is 7.8133 hours per week. The standard deviation of the exercise time is 5.8032, indicating that there is some variability in the data.
To determine whether the claim that the mean exercise time of all students is 10 hours per week is reasonable, we can conduct a hypothesis test.
Our null hypothesis would be that the mean exercise time of all students is equal to 10 hours per week, and the alternative hypothesis would be that the mean exercise time is different from 10 hours per week.
We can then calculate a test statistic and compare it to a critical value based on a t-distribution with n-1 degrees of freedom, where n is the sample size.
Alternatively, we can use the confidence interval provided in the table to make a statement about the claim.
We can see that the 95% confidence interval for the mean exercise time is [7.0769, 8.5497]. Since 10 is outside of this interval, we can say that at the 95% confidence level, the claim that the mean exercise time of all students is 10 hours per week is not supported by the data.
Therefore, the most appropriate response to the claim would be: "At the 95% confidence level, the mean exercise time of all students might not be 10 hours per week based on the sample data."
Learn more about confidence level.
brainly.com/question/22851322
#SPJ11
6²
Which theorem is shown by the diagram above?
a + b = c
C
D
a - b = c
a² + b² = c²
a²-b² = c²
Answers
The theorem is shown in a pythagoras theorem is c² = a² + b²
Which theorem is shown in a pythagoras theoremThe theorem shown in the Pythagorean theorem is "a² + b² = c²". This theorem is named after the ancient Greek mathematician Pythagoras, who is credited with discovering it.
The Pythagorean theorem applies to right-angled triangles and states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Mathematically, we can express this as:
c² = a² + b²
Where c is the length of the hypotenuse, and a and b are the lengths of the other two sides (called the legs) of the right-angled triangle.
Read more about pythagoras theorem at
https://brainly.com/question/231802
#SPJ1
4. The radius of a cylinder is 3x-2 cm. The height of the cylinder is x +3 cm. What is the
surface area of the cylinder? Use the formula A=2x²+2xrh.
02x (3x2+10x-8)
O 27(12x+7x-2)
O 27(12x²-2x+13)
O 27(12x²-5x-2)
Answers
Answer:
D: 27(12x² - 5x - 2).
Step-by-step explanation:
The formula for the surface area of a cylinder is: A = 2πr² + 2πrh
Given that the radius of the cylinder is 3x - 2 cm and the height is x + 3 cm, we can substitute these values in the formula and simplify:
A = 2π(3x - 2)² + 2π(3x - 2)(x + 3)
A = 2π(9x² - 12x + 4) + 2π(3x² + 7x - 6)
A = 18πx² - 24πx + 8π + 6πx² + 14πx - 12π
A = 24πx² - 10πx - 4π
A = 2π(12x² - 5x - 2)
Therefore, the answer is option D: 27(12x² - 5x - 2).
Answer:
D
Step-by-step explanation:
the table shows several packages of assorted spools of thread available at a store. what is the price per spool of each kind of thread?
Answers
I'm sorry, but I cannot provide a definitive answer to your question as I do not have access to the table you are referring to.
However, in general, to find the price per spool of each kind of thread, you would need to know the total price of the package and the number of spools in the package.
To calculate the price per spool, you would divide the total price of the package by the number of spools in the package. For example, if a package costs $10 and contains 50 spools of thread, the price per spool would be $0.20 ($10 ÷ 50 = $0.20).
You can use this method to find the price per spool for each type of thread in the table you are looking at.
For more questions like Spool visit the link below:
https://brainly.com/question
#SPJ11
i need some help with this problem i don’t really understand it
Answers
Answer:
-34x+29
Step-by-step explanation:
[tex]7(5-x)-3(9x+2)=7.5-7x-3.9x-3.2=35-7x-27x-6\\=-34x+29[/tex]
How do you find the period of a cosine function of the form y = cos bx?
Answers
The period of a cosine function of the form y = cos bx is equal to T= 2π/b where 'T' is the period of the cosine function and b is the coefficient of x in the function.
This formula tells us that the period of the cosine function is equal to the length of one complete cycle of the function.
it represents the distance along the x-axis for the cosine function to complete one full oscillation.
The period of a cosine function of the form y = cos bx, first identify the coefficient b.
Use the formula T= 2π/b to calculate the period 'T'.
For example,
Consider cosine function y = cos 2x,
The coefficient of x is 2.
Using the formula above, the period is equal to
Period = 2π/2
= π
So the period of the function y = cos 2x is π.
This implies that the cosine function completes one full oscillation every π units along the x-axis.
Therefore, the formula used to calculate the period of the cosine function y = cos bx is given by T= 2π/b.
learn more about period here
brainly.com/question/3649898
#SPJ4
What is the mean of this data set?
Please help
Answers
Answer:
Step-by-step explanation:
Find the area of the circle with a circumference of
. Write your solution in terms of
.
Area in terms of
: ______
if you used this version of the equation (including your new conversion factor, how would this have changed the intercept of your log-log graph? what would its value have been?
Answers
The equation with the new substitutions and conversion factor is a'B'T' = (1/6) * (2/3)^(1/3) * a^(1/3) * d^(1/2)*a^6/6 where k is (1/6) * (2/3)^(1/3) * a^(1/3) * d^(1/2) The intercept value of the log-log graph would have been -1.108.
Starting with Equation 4: T = ka^6/6, we can substitute a = (d/k)^(1/6) and b = (2/3)^(1/2) * (d/k)^(1/3) to get
T = k[(d/k)^(1/6)]^6/6
T = k(d/k)^(1/2)/6
T = (k^(1/2)/6) * d^(1/2)
Now we can rearrange the equation so that a, b, and t are on the left side
a'B'T' = ka^6/6
(a/d)^(1/6) * b^(2/3) * T' = k[(a/d)^(1/6)]^6/6 * T'
(a/d)^(1/6) * (2/3)^(1/2) * (d/k)^(1/3) * T' = (k^(1/2)/6) * d^(1/2) * T'
(2/3)^(1/2) * (a/d)^(1/6) * d^(1/3) * T' = (k^(1/2)/6) * d^(1/2) * T'
(2/3)^(1/2) * (a/d)^(1/6) * d^(1/3) = k^(1/2)/6
k = [(2/3)^(1/2) * (a/d)^(1/6) * d^(1/3)]^2/6
k = (1/6) * (2/3)^(1/3) * a^(1/3) * d^(1/2)
With this new conversion factor, the intercept of the log-log graph would have changed. The intercept represents the value of T when a = 1 (since log(1) = 0). Using the new conversion factor, we have
T = (1/6) * (2/3)^(1/3) * d^(1/2) * a^(1/3)
T = (1/6) * (2/3)^(1/3) * d^(1/2)
log(T) = log[(1/6) * (2/3)^(1/3) * d^(1/2)]
log(T) = log(1/6) + log[(2/3)^(1/3)] + log(d^(1/2))
log(T) = log(1/6) + (1/3) * log(2/3) + (1/2) * log(d)
So the intercept of the log-log graph would be log(1/6) + (1/3) * log(2/3) = -1.108, assuming that d is held constant. This intercept represents the value of log(T) when log(a) = 0, or when a = 1. In other words, when a = 1, the predicted value of T would be 0.162 (or 16.2% of its maximum value).
To know more about log graph:
https://brainly.com/question/17009226
#SPJ4
--The given question is incomplete, the complete question is given
" Plug the two substitutions into Equation 4 (T = ka^6/6)). Rearrange the equation so that a, b,t are on the left side of the equation and d remains on the right side, e.g. a'B'T' = ka^6/6 you will figure out what the "k" if you used this version of the equation (including your new conversion factor, how would this have changed the intercept of your log-log graph? what would its value have been?"--
One gallon of paint covers 400 square feet. What is the least amount of paint needed to paint the walls of a room in the shape of a rectangular prism with a length of 17 feet, a width of 15 feet, and a height of 12 feet? Write your answer as a decimal. Gal
Answers
We need at least 3.465 gallons of paint to paint the walls of this room.
The area of the two rectangular faces on either end of the prism is:
length x height = 17 x 12 = 204 square feet
The area of the two rectangular faces on the sides of the prism is:
width x height = 15 x 12 = 180 square feet
The area of the top and bottom faces of the prism is:
length x width = 17 x 15 = 255 square feet
The total surface area of the prism is:
2(204) + 2(180) + 2(255) = 1386 square feet
Now, we divide surface area by coverage of one gallon of paint:
1386 / 400 = 3.465
To know more about surface area , here
brainly.com/question/29298005
#SPJ4
rewrite the following without an exponent 4^-3
Answers
Step-by-step explanation:
4^-3 = 1/4^3 = 1/64